
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 的斜率为1的切线方程;
的斜率为1的切线方程;
(Ⅱ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅲ)设![]() ,记
,记![]() 在区间
在区间![]() 上的最大值为M(a),当M(a)最小时,求a的值.
上的最大值为M(a),当M(a)最小时,求a的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某行业主管部门为了解本行业中小企业的生产情况,随机调查了100个企业,得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(2)求这类企业产值增长率的平均数与标准差的估计值(同一组中的数据用该组区间的中点值为代表).(精确到0.01)
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;
”;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③![]() 命题“,使得
命题“,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”;
”;
④命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
其中所有正确命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,![]() 是锐角,大小为β.图中阴影区域的面积的最大值为
是锐角,大小为β.图中阴影区域的面积的最大值为
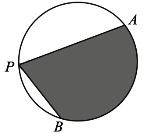
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】男运动员![]() 名,女运动员
名,女运动员![]() 名,其中男女队长各
名,其中男女队长各![]() 人,选派
人,选派![]() 人外出比赛,在下列情形中各有多少种选派方法.
人外出比赛,在下列情形中各有多少种选派方法.
(1)任选![]() 人
人
(2)男运动员![]() 名,女运动员
名,女运动员![]() 名
名
(3)至少有![]() 名女运动员
名女运动员
(4)队长至少有一人参加
(5)既要有队长,又要有女运动员
查看答案和解析>>
科目:高中数学 来源: 题型:
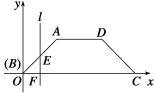
【题目】如图所示,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2![]() cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
cm,当一条垂直于底边BC(垂足为F)的直线l从B点开始由左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x(0≤x≤7),左边部分的面积为y,求y与x之间的函数关系式,画出程序框图,并写出程序.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,一艺术拱门由两部分组成,下部为矩形![]() ,
,![]() 的长分别为
的长分别为![]() 和
和![]() ,上部是圆心为
,上部是圆心为![]() 的劣弧
的劣弧![]() ,
,![]() .
.
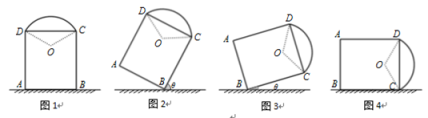
(1)求图1中拱门最高点到地面的距离;
(2)现欲以B点为支点将拱门放倒,放倒过程中矩形![]() 所在的平面始终与地面垂直,如图2、图3、图4所示.设
所在的平面始终与地面垂直,如图2、图3、图4所示.设![]() 与地面水平线
与地面水平线![]() 所成的角为
所成的角为![]() .记拱门上的点到地面的最大距离为
.记拱门上的点到地面的最大距离为![]() ,试用
,试用![]() 的函数表示
的函数表示![]() ,并求出
,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() 单位:万只
单位:万只![]() 与相应年份
与相应年份![]() 序号
序号![]() 的数据表和散点图
的数据表和散点图![]() 如图所示
如图所示![]() ,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数
,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数![]() 单位:个
单位:个![]() 关于x的回归方程
关于x的回归方程![]() .
.
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊 |
|
|
|
|
|
|
|
|
|
![]() 根据表中的数据和所给统计量,求y关于x的线性回归方程
根据表中的数据和所给统计量,求y关于x的线性回归方程![]() 参考统计量:
参考统计量:![]() ,
,![]() ;
;
![]() 试估计:
试估计:![]() 该县第一年养殖山羊多少万只
该县第一年养殖山羊多少万只
![]() 到第几年,该县山羊养殖的数量与第一年相比缩小了?
到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com