
分析 (1)由题意可得a<$\sqrt{3}b$,由列举法求出事件A包含的基本事件个数m=6+5+4+3+2+1=21,而总的方法种数为n=6×6=36,由此能求出事件A发生的概率.
(Ⅱ)依题意为几何概型,a<$\sqrt{3}$b与(a-$\sqrt{3}$)2+(b-1)2≤4的公共面积为直线a=$\sqrt{3}b$与圆(a-$\sqrt{3}$)2+(b-1)2=4相交的弓形的面积,由点到直线的距离公式可得圆心($\sqrt{3}$,1)在直线a=$\sqrt{3}b$上,由此能求出事件A发生的概率.
解答 解:(1)由题意可得:直线ax-by=0与圆(x-2$\sqrt{2}$)2+y2=6相交,
所以圆心(2$\sqrt{2}$,0)到直线的距离d=$\frac{|2\sqrt{2}a|}{\sqrt{{a}^{2}+{b}^{2}}}$<$\sqrt{6}$,即a2<3b2,
又a、b均大于0,故a<$\sqrt{3}b$,
当a=1时,b=1,2,3,4,5,6;当a=2时,b=2,3,4,5,6;当a=3时,b=3,4,5,6;
当a=4时,b=4,5,6;当a=5时,b=5,6;当a=6时,b=6.
∴事件A包含的基本事件个数m=6+5+4+3+2+1=21,
而总的方法种数为n=6×6=36
故事件A发生的概率为P(A)=$\frac{m}{n}$=$\frac{21}{36}$=$\frac{7}{12}$.
(Ⅱ)依题意为几何概型,a<$\sqrt{3}$b与(a-$\sqrt{3}$)2+(b-1)2≤4的公共面积为:
直线a=$\sqrt{3}b$与圆(a-$\sqrt{3}$)2+(b-1)2=4相交的弓形的面积,
由点到直线的距离公式可得:
圆心($\sqrt{3}$,1)到直线a=$\sqrt{3}b$的距离d′=0,
∴直线a=$\sqrt{3}b$与圆(a-$\sqrt{3}$)2+(b-1)2=4相交的弓形的面积为圆的面积的一半,
∴事件A发生的概率P(A)=$\frac{1}{2}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线距离公式、列举法和几何概型的合理运用.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
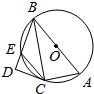 如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④.
如图,在△ABC中,∠ACB=90°,AB=2AC=8,作△ABC外接圆O的切线CD,作BD⊥CD于D,交圆O于点E,给出下列四个结论:①∠BCD=60°;②DE=2;③BC2=BD•BA;④CE∥AB;则其中正确的序号是①②③④.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
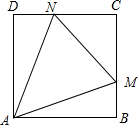 如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )| A. | 4($\sqrt{2}$-1) | B. | 8($\sqrt{2}$-1) | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com