
【题目】近年来,某地区积极践行“绿水青山就是金山银山”的绿色发展理念![]() 年年初至
年年初至![]() 年年初,该地区绿化面积
年年初,该地区绿化面积![]() (单位:平方公里)的数据如下表:
(单位:平方公里)的数据如下表:
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
绿化面积 |
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测该地区![]() 年年初的绿化面积,并计算
年年初的绿化面积,并计算![]() 年年初至
年年初至![]() 年年初,该地区绿化面积的年平均增长率约为多少.
年年初,该地区绿化面积的年平均增长率约为多少.
(附:回归直线的斜率与截距的最小二乘法估计公式分别为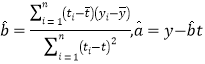 ,
,![]() )
)
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,圆
,圆![]() .
.
(1)求![]() 的取值范围,并求出圆心坐标;
的取值范围,并求出圆心坐标;
(2)有一动圆![]() 的半径为
的半径为![]() ,圆心在
,圆心在![]() 上,若动圆
上,若动圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·吉林期末]一个袋中装有6个大小形状完全相同的球,球的编号分别为1,2,3,4,5,6.
(1)从袋中随机抽取两个球,求取出的球的编号之和为6的概率;
(2)先后有放回地随机抽取两个球,两次取的球的编号分别记为![]() 和
和![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抽取彩票“双色球”中奖号码时,有33个红色球,每个球的编号分别为01,02,…,33.一位彩民用随机数表法选取6个号码作为6个红色球的编号,选取方法是从下面的随机数表中第1行第6列的数字3开始,从左向右读数,则依次选出的第3个红色球的编号为( )
49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64 |
57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
A.21B.32C.09D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的上焦点
,以椭圆的上焦点![]() 为圆心,椭圆的短半轴为半径的圆与直线
为圆心,椭圆的短半轴为半径的圆与直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆的方程;
(2)过椭圆左顶点做两条互相垂直的直线![]() ,
,![]() ,且分别交椭圆于
,且分别交椭圆于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 不是椭圆的顶点),探究直线
不是椭圆的顶点),探究直线![]() 是否过定点,若过定点则求出定点坐标,否则说明理由.
是否过定点,若过定点则求出定点坐标,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
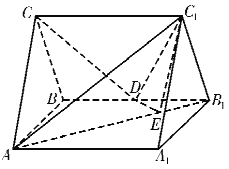
(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求点
所成的角为45°,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com