Question

20．过点A（-1，0）且斜率为k（k＞0）的直线与抛物线y²=4x相交于B，C两点，若|AB|=$\frac{1}{3}$|BC|，则k等于（　　）

• A． 1
• B． $\frac{1}{2}$
• C． $\frac{4}{5}$
• D． $\frac{3}{4}$

Answer 1

分析 根据题意表示出直线方程，代入抛物线方程消去x，利用求根公式求出B，C的纵坐标，利用|AB|=$\frac{1}{3}$|BC|，建立等式，把A，B的纵坐标带入即可求得k．

解答 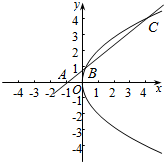解：依题意知直线方程为y=k（x+1），代入抛物线方程，整理得ky²-4y+4k=0，
解得y_B=$\frac{2-2\sqrt{1-{k}^{2}}}{k}$，y_C=$\frac{2+2\sqrt{1-{k}^{2}}}{k}$，
∵|AB|=$\frac{1}{3}$|BC|，∴y_B=$\frac{1}{4}$y_C，
∴$\frac{2-2\sqrt{1-{k}^{2}}}{k}$=$\frac{1}{4}$•$\frac{2+2\sqrt{1-{k}^{2}}}{k}$，
∵k＞0，∴求得k=$\frac{4}{5}$．
故选：C．

点评 本题主要考查了直线与抛物线的位置关系．一般解法是设出直线方程，与抛物线方程联立进行消元，利用转化为一元二次方程的问题进行解决．