
(1)3只全是红球的概率;
(2)3只颜色全相同的概率;
(3)3只颜色不全相同的概率;
(4)3只颜色全不相同的概率.
解析:利用互斥事件和对立事件概率公式求概率.?
(1)记“3只全是红球”的事件为A,从袋中有放回地抽取3次,每次取1只,共会出现3×3×3=27种等可能的结果,其中3只全是红球的只有一种,故事件A的概率为P(A)=![]() .?
.?
(2)“3只颜色全相同”只可能有三种情况,“三只全是红球”记为事件A,“三只全是黄球”记为事件B,“三只全是白球”记为事件C,由于它们不能同时发生,是彼此互斥事件,由(1)得P(B)=P(C)=P(A)= ![]() ,所以P(A+B+C)=P(A)+P(B)+P(C)=
,所以P(A+B+C)=P(A)+P(B)+P(C)=![]() .?
.?
(3)3只颜色不全相同的情况较多,可以是两只黄球一只白球,也可以是两只白球一只红球或是三种颜色各一只.考虑进来比较麻烦,现记“3只颜色不全相同”为事件D,则事件D为“3只颜色全相同”,显然用对立事件的概率来求比较方便,所以P(D)=1-P(![]() )=1-
)=1-![]() =
=![]() .?
.?
(4)要使3只颜色全不相同,只可能是红、黄、白球各一只,要分三次抽取,故3次抽到红、黄、白球各一只的可能结果为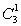
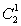
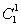 =6种或A33=6种,故三只颜色全不相同的概率为P(E)=
=6种或A33=6种,故三只颜色全不相同的概率为P(E)=![]() .
.
答案:(1)![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ;(4)
;(4)![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
(1)3只全是红球的概率;
(2)3只颜色全相同的概率;
(3)3只颜色不全相同的概率;
(4)3只颜色全不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)3个全是红球的概率;
(2)3个颜色全相同的概率;
(3)3个颜色不全相同的概率;
(4)3个颜色全不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)3只全是红球的概率;
(2)3只颜色全相同的概率;
(3)3只颜色不全相同的概率;
(4)3只颜色全不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)3只全是红球的概率;
(2)3只颜色全相同的概率;
(3)3只颜色不全相同的概率;
(4)3只颜色全不相同的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com