
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形, ![]() ,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
,AB⊥AD,AB∥CD,点M是PC的中点. (I)求证:MB∥平面PAD;
(II)求二面角P﹣BC﹣D的余弦值.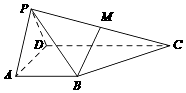
【答案】证明:(Ⅰ)取PD中点H,连结MH,AH. 因为 M为 ![]() 中点,所以
中点,所以 ![]() .
.
因为 ![]() .所以AB∥HM且AB=HM.
.所以AB∥HM且AB=HM.
所以四边形ABMH为平行四边形,所以 BM∥AH.
因为 BM平面PAD,AH平面PAD,
所以BM∥平面PAD.
解:(Ⅱ) 取AD中点O,连结PO.
因为 PA=PD,所以PO⊥AD.
因为 平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,PO平面PAD,
所以PO⊥平面ABCD.取BC中点K,连结OK,则OK∥AB.
以O为原点,如图建立空间直角坐标系,
设AB=2,则 ![]() ,
, ![]() .
.
平面BCD的法向量 ![]() ,
,
设平面PBC的法向量 ![]() ,
,
由 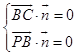 ,得
,得 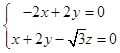 令x=1,则
令x=1,则 ![]() .
.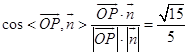 .
.
由图可知,二面角P﹣BC﹣D是锐二面角,
所以二面角P﹣BC﹣D的余弦值为 ![]() .
.
【解析】(Ⅰ)取PD中点H,连结MH,AH.推导出四边形ABMH为平行四边形,从而BM∥AH,由此能证明BM∥平面PAD.(Ⅱ) 取AD中点O,连结PO.以O为原点,建立空间直角坐标系,利用向量法能求出二面角P﹣BC﹣D的余弦值.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( ) 
A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线PD与平面ABC所成的角为45°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两煤矿每年的产量分别为200万吨和260万吨,需经过东车站和西车站两个车站运往外地.东车站每年最多能运280万吨煤,西车站毎年最多能运360万吨煤,甲煤矿运往东车站和西车站的运费价格分别为1元/t和1.5元/t,乙煤矿运往东车站和西车站的运费价格分别为0.8元/t和1.6元/t.煤矿应怎样编制调运方案,能使总运费最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正项等差数列{an}中a1和a4是方程x2﹣10x+16=0的两个根,若数列{log2an}的前5项和为S5且S5∈[n,n+1],n∈Z,则n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题: ①“若a2<b2 , 则a<b”的否命题;
②“全等三角形面积相等”的逆命题;
③“若a>1,则ax2﹣2ax+a+3>0的解集为R”的逆否命题;
④“若 ![]() x(x≠0)为有理数,则x为无理数”的逆否命题.
x(x≠0)为有理数,则x为无理数”的逆否命题.
其中正确的命题是( )
A.③④
B.①③
C.①②
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查某车间20名工人的年龄,第i名工人的年龄为ai,具体数据见表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ai | 29 | 28 | 30 | 19 | 31 | 28 | 30 | 28 | 32 | 31 | 30 | 31 | 29 | 29 | 31 | 32 | 40 | 30 | 32 | 30 |
(1)作出这20名工人年龄的茎叶图;
(2)求这20名工人年龄的众数和极差;
(3)执行如图所示的算法流程图(其中 ![]() 是这20名工人年龄的平均数),求输出的S值.
是这20名工人年龄的平均数),求输出的S值. 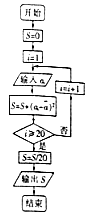
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个内角A、B、C所对的边分别为a、b、c,1+ ![]() =
= ![]() .
.
(1)求A的大小;
(2)若△ABC为锐角三角形,求函数y=2sin2B﹣2cosBcosC的取值范围;
(3)现在给出下列三个条件:①a=1;②2c﹣( ![]() +1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
+1)b=0;③B=45°,试从中再选择两个条件,以确定△ABC,求出所确定的△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某位篮球运动员8场比赛得分的茎叶图,其中一个数据染上污渍用x代替,则这位运动员这8场比赛的得分平均数不小于得分中位数的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com