
| A. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{6}$ | B. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{6}$ | ||
| C. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{12}$ | D. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{12}$ |
分析 将x=$\frac{π}{4}$代入得:t=$\frac{1}{2}$,进而求出平移后P′的坐标,进而得到s的最小值.
解答 解:将x=$\frac{π}{4}$代入得:t=sin$\frac{π}{6}$=$\frac{1}{2}$,进而求出平移后P′的坐标,
将函数y=sin(x-$\frac{π}{12}$)图象上的点P($\frac{π}{4}$,t)向左平移s(s>0)个单位,
得到点P′,若P′位于函数y=sin2x的图象上,
则sin($\frac{π}{2}$+2s)=cos2s=$\frac{1}{2}$,
则2s=±$\frac{π}{3}$+2kπ,k∈Z,
则s=±$\frac{π}{6}$+kπ,k∈Z,
由s>0得:当k=0时,s的最小值为$\frac{π}{6}$,
故选:A.
点评 本题考查的知识点是函数y=Asin(ωx+φ)(A>0,ω>0)的图象和性质,难度中档.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:选择题
 一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )
一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )| A. | $\frac{19}{6}$ | B. | $\frac{38}{3}$ | C. | $\frac{57}{8}$ | D. | $\frac{19}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
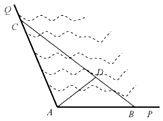 如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.
如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,5] | B. | (-∞,5] | C. | {1,2,3,4,5} | D. | {2,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com