练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设x，y满足约束条件 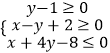，且目标函数z=ax+y仅在点（4，1）处取得最大值，则原点O到直线ax﹣y+17=0的距离d的取值范围是（ ）
    A.（4 ，17]
    B.（0，4 ）
    C.（ ，17]
    D.（0， ）

    【答案】B
    【解析】解：∵约束条件 作出可行域，如右图可行域，

    ∵目标函数z=ax+y仅在点A（4，1）取最大值，

    当a=0时，z=y仅在y=1上取最大值，不成立；

    当a＜0时，目标函数z=ax+y的斜率k=﹣a＞0，

    目标函数在（4，1）取不到最大值．

    当a＞0时，目标函数z=ax+y的斜率k=﹣a，小于直线x+4y﹣8=0的斜率﹣ ，∴a＞ ．

    综上， ＜a．

    原点O到直线ax﹣y+17=0的距离d= ＜4

    则原点O到直线ax﹣y+17=0的距离d的取值范围是：（0，4 ）

    所以答案是：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=（ ）
    A.
    B.8
    C.
    D.10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设p：实数x满足x2﹣4ax+3a2＜0（a＞0）；命题q：实数x满足
    （1）若a=1，且“p且q”为真，求实数x的取值范围
    （2）若￢p是￢q的充分不必要条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设△ABC的内角A，B，C所对的边分别为a，b，c且acosB=4，bsinA=3．
    （1）求tanB及边长a的值；
    （2）若△ABC的面积S=9，求△ABC的周长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知不等式|x+2|+|x﹣2|＜18的解集为A．
    （1）求A；
    （2）若a，b∈A，x∈（0，+∞），不等式a+b＜x +m恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，已知2sinA﹣cosB=2sinBcosC，且角B为钝角．
    （1）求角C的大小；
    （2）若a=2，b2+c2﹣a2= bc，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如何把一条长为m的绳子截成3段，各围成一个正方形，使这3个正方形的面积和最小？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，MCN是某海湾旅游区的一角，为营造更加优美的旅游环境，旅游区管委会决定建立面积为4 平方千米的三角形主题游戏乐园ABC，并在区域CDE建立水上餐厅．已知∠ACB=120°，∠DCE=30°．
    （1）设AC=x，AB=y，用x表示y，并求y的最小值；
    （2）设∠ACD=θ（θ为锐角），当AB最小时，用θ表示区域CDE的面积S，并求S的最小值．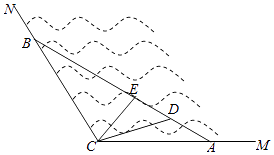

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：（x+2）2+y2=5，直线l：mx﹣y+1+2m=0，m∈R．
    （1）求证：对m∈R，直线l与圆C总有两个不同的交点A、B；
    （2）求弦AB的中点M的轨迹方程，并说明其轨迹是什么曲线；
    （3）是否存在实数m，使得圆C上有四点到直线l的距离为 ？若存在，求出m的范围；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案