
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).M是曲线
为参数).M是曲线![]() 上的动点,将线段OM绕O点顺时针旋转
上的动点,将线段OM绕O点顺时针旋转![]() 得到线段ON,设点N的轨迹为曲线
得到线段ON,设点N的轨迹为曲线![]() .以坐标原点O为极点,
.以坐标原点O为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,若射线![]() 与曲线
与曲线![]() 分别交于A, B两点(除极点外),且有定点
分别交于A, B两点(除极点外),且有定点![]() ,求
,求![]() 的面积.
的面积.
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数,![]() 且
且![]() ),且数列
),且数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,当
,当![]() 时,求数列
时,求数列![]() 的前
的前![]() 项和
项和![]() 的最小值;
的最小值;
(3)若![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 是递增数列?若存在,求出
是递增数列?若存在,求出![]() 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴![]() 的交点为
的交点为![]() ,与
,与![]() 轴正方向同向的单位向量分别是
轴正方向同向的单位向量分别是![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,其中
,其中![]() 。由平面向量基本定理,对于平面内的向量
。由平面向量基本定理,对于平面内的向量![]() ,存在唯一有序实数对
,存在唯一有序实数对![]() ,使得
,使得![]() ,把
,把![]() 叫做点
叫做点![]() 在斜坐标系
在斜坐标系![]() 中的坐标,也叫做向量
中的坐标,也叫做向量![]() 在斜坐标系
在斜坐标系![]() 中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如
中的坐标。在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如![]() 时,方程
时,方程![]() 表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。
表示斜坐标系内一条过点(2,1),且方向向量为(4,-5)的直线。
(1)若![]() ,
,![]() ,且
,且![]() 与
与![]() 的夹角为锐角,求实数m的取值范围;
的夹角为锐角,求实数m的取值范围;
(2)若![]() ,已知点
,已知点![]() 和直线
和直线![]() ①求l的一个法向量;②求点A到直线l的距离。
①求l的一个法向量;②求点A到直线l的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量( | 1 | 2 | 3 | 5 | 7 | 9 |
弹簧长度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)请在下图坐标系中画出上表所给数据的散点图;

(2)若弹簧长度与所挂物体重量之间的关系具有线性相关性,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据回归方程,求挂重量为![]() 的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
注:本题中的计算结果保留小数点后两位.
(参考公式: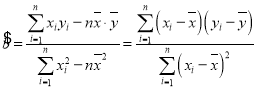 ,
,![]() )
)
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为![]() ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( )

A. “弦”![]() 米,“矢”
米,“矢”![]() 米
米
B. 按照经验公式计算所得弧田面积(![]() )平方米
)平方米
C. 按照弓形的面积计算实际面积为(![]() )平方米
)平方米
D. 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据![]()
![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com