
【题目】已知向量 ![]() =(sinx,
=(sinx, ![]() ),
), ![]() =(cosx,﹣1).
=(cosx,﹣1).
(1)当 ![]() ∥
∥ ![]() 时,求tan(x﹣
时,求tan(x﹣ ![]() )的值;
)的值;
(2)设函数f(x)=2( ![]() +
+ ![]() )
) ![]() ,当x∈[0,
,当x∈[0, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
科目:高中数学 来源: 题型:
【题目】(2009年广东卷文)某单位200名职工的年龄分布情况如图2,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号…,196-200号).若第5组抽出的号码为22,则第8组抽出的号码应是 。若用分层抽样方法,则40岁以下年龄段应抽取 人.

图 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟,课后研讨20分钟,可获得学分5分B套选修课播32分钟,课后研讨40分钟,可获学分4分。全学期20周,网络每周开播两次,每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟,研讨时间不得少于1000分钟。两套选修课怎样合理选择,才能获得最好学分成绩?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米. 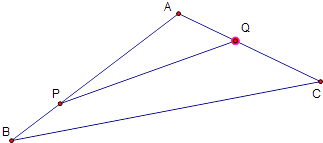
(1)当x,y为何值时?游客体验活动区APQ的面积最大,并求最大面积;
(2)当x,y为何值时?线段|PQ|最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是(﹣1,1)上的偶函数,且在区间(﹣1,0)上是单调递增的,A,B,C是锐角三角形△ABC的三个内角,则下列不等式中一定成立的是( )
A.f(sinA)>f(sinB)
B.f(sinA)>f(cosB)
C.f(cosC)>f(sinB)
D.f(sinC)>f(cosB)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com