
【题目】如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.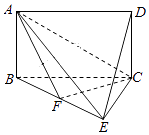
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上,若DE∥平面ACF,DC=CE= ![]() BC=3,求三棱锥A﹣BCF的体积.
BC=3,求三棱锥A﹣BCF的体积.
【答案】
(1)证明:∵ABCD为矩形,∴AB⊥BC.
∵平面ABCD⊥平面BCE,平面ABCD∩平面BCE=BC,AB平面ABCD,
∴AB⊥平面BCE.
∵CE平面BCE,∴CE⊥AB.
∵CE⊥BE,AB平面ABE,BE平面ABE,AB∩BE=B,
∴CE⊥平面ABE.
∵CE平面AEC,∴平面AEC⊥平面ABE.
(2)解:连接BD交AC于点O,连接OF.
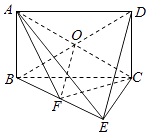
∵DE∥平面ACF,DE平面BDE,平面ACF∩平面BDE=OF,
∴DE∥OF.
又∵矩形ABCD中,O为BD中点,
∴F为BE中点,即BF=FE.
在Rt△BEC中,∵BC=6,EC=3,∴BE= ![]() .
.
∴ ![]() .
.
又AB=DC=3.
∴ ![]() .
.
【解析】1、根据面面垂直的性质定理可得AB⊥平面BCE,即得CE⊥AB,再根据线面垂直的判定定理可得到CE⊥平面ABE,故得到平面AEC⊥平面ABE.
2、由线面平行的性质定理可得DE∥OF,再利用已知可得BF=FE,利用等体积法可求出 V A-BCF.


科目:高中数学 来源: 题型:
【题目】已知cos(π+α)= ![]() ,且
,且 ![]() <α<π.
<α<π.
(Ⅰ)求5sin(α+π)﹣4tan(3π﹣α)的值
(Ⅱ)若0<β< ![]() ,cos(β﹣α)=
,cos(β﹣α)= ![]() ,求sin(
,求sin( ![]() +2β)的值.
+2β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=(logmx)2+2logmx﹣3(m>0,且m≠1).
(Ⅰ)当m=2时,解不等式f(x)<0;
(Ⅱ)f(x)<0在[2,4]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={1,2,3,4,5,6,7,8,9,10,11,12},以下命题正确的序号是 .
①如果函数f(x)=x(x﹣a1)(x﹣a2)…(x﹣a7),其中ai∈M(i=1,2,3,…,7),那么f′(0)的最大值为127 .
②数列{an}满足首项a1=2,ak+12﹣ak2=2,k∈N* , 当n∈M且n最大时,数列{an}有2048个.
③数列{an}(n=1,2,3,…,8)满足a1=5,a8=7,|ak+1﹣ak|=2,k∈N* , 如果数列{an}中的每一项都是集合M的元素,则符合这些条件的不同数列{an}一共有33个.
④已知直线amx+any+ak=0,其中am , an , ak∈M,而且am<an<ak , 则一共可以得到不同的直线196条.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com