
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 7 |
分析 作OD⊥AB于D,OE⊥AC于E,利用圆的弦的性质可得AD=$\frac{1}{2}•AB$,求得$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{{AB}^{2}}{2}$,同理可得$\overrightarrow{AO}•\overrightarrow{AC}$=$\frac{{AC}^{2}}{2}$,从而求得$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\overrightarrow{AO}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)的值.
解答 解: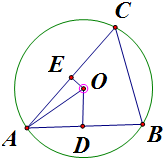 作OD⊥AB于D,OE⊥AC于E,
作OD⊥AB于D,OE⊥AC于E,
∵⊙O中,OD⊥AB,∴AD=$\frac{1}{2}•AB$,cos∠OAD=$\frac{AD}{AO}$,
∴$\overrightarrow{AO}•\overrightarrow{AB}$=AO•AB•cos∠OAD=$\frac{{AB}^{2}}{2}$=2,
同理可得$\overrightarrow{AO}•\overrightarrow{AC}$=$\frac{{AC}^{2}}{2}$=$\frac{9}{2}$,
∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=$\overrightarrow{AO}$•($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\overrightarrow{AO}•\overrightarrow{AC}$-$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{9}{2}$-2=$\frac{5}{2}$,
故选:B.
点评 本题给出三角形的外接圆的圆心为0,在已知三边长的情况下求$\overrightarrow{AO}•\overrightarrow{BC}$的值,着重考查了圆中垂直于弦的直径性质、三角函数在直角三角形中的定义和向量数量积公式及其性质等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$或$\frac{11}{32}$ | B. | $\frac{1}{2}$或$\frac{31}{32}$ | C. | $\frac{11}{32}$或$\frac{31}{32}$ | D. | $\frac{11}{32}$或$\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,+∞) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三角形的边长与面积之间的关系 | |
| B. | 等边三角形的边长与面积之间的关系 | |
| C. | 四边形的边长与面积之间的关 | |
| D. | 菱形的边长与面积之间的关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(|x|)=x+1 | B. | f(x2)=2x+1 | C. | f(|x|)=x2+2 | D. | f($\sqrt{x}$)=3x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (ln2,1) | B. | ($\frac{1}{2}$,ln2) | C. | ($\frac{1}{3}$,$\frac{1}{e}$) | D. | ($\frac{1}{e}$,$\frac{1}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com