
【题目】下列命题中正确的命题个数是( )
①. 如果![]() 共面,
共面, ![]() 也共面,则
也共面,则![]() 共面;
共面;
②.已知直线a的方向向量![]() 与平面
与平面![]() ,若
,若![]() //
// ![]() ,则直线a//
,则直线a// ![]() ;
;
③若![]() 共面,则存在唯一实数
共面,则存在唯一实数![]() 使
使![]() ,反之也成立;
,反之也成立;
④.对空间任意点O与不共线的三点A、B、C,若![]() =x
=x![]() +y
+y![]() +z
+z![]()
(其中x、y、z∈R),则P、A、B、C四点共面.
A. 3 B. 2 C. 1 D. 0
科目:高中数学 来源: 题型:
【题目】如图,在菱形![]() 中,
中, ![]() ,
, ![]() ,以4个顶点为圆心的扇形的半径为1,若在该菱形中任意选取一点,该点落在阴影部分的概率为
,以4个顶点为圆心的扇形的半径为1,若在该菱形中任意选取一点,该点落在阴影部分的概率为![]() ,则圆周率
,则圆周率![]() 的近似值为( )
的近似值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】因为菱形的内角和为360°,
所以阴影部分的面积为半径为1的圆的面积,
故由几何概型可知 ,
,
解得![]() .选C。
.选C。
【题型】单选题
【结束】
12
【题目】已知函数f(x)= ,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
,若g(x)=f(x)-a恰好有3个零点,则a的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义域为R的奇函数,当x∈[0,+∞)时,f(x)=x2-2x.
(1)写出函数y=f(x)的解析式
(2)若方程f(x)=a恰有3个不同的解,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2ωx﹣ ![]() )(ω>0)的最小正周期为4π,则( )
)(ω>0)的最小正周期为4π,则( )
A.函数f(x)的图象关于点( ![]() ,0)对称
,0)对称
B.函数f(x)的图象关于直线x= ![]() 对称
对称
C.函数f(x)的图象在( ![]() ,π)上单调递减
,π)上单调递减
D.函数f(x)的图象在( ![]() ,π)上单调递增
,π)上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 6 | 7 | 8 | 9 | 10 |
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)用所求回归方程预测该地区2015年![]() 的人民币储蓄存款.
的人民币储蓄存款.
附:回归方程![]() 中,
中, 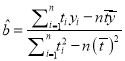 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx+cos2x,x∈R.
sinxcosx+cos2x,x∈R.
(1)把函数f(x)的图象向右平移 ![]() 个单位,得到函数g(x)的图象,求g(x)在[0,
个单位,得到函数g(x)的图象,求g(x)在[0, ![]() ]上的最大值;
]上的最大值;
(2)在△ABC中,角A,B,C对应的三边分别为a,b,c,b= ![]() ,f(
,f( ![]() )=1,S△ABC=3
)=1,S△ABC=3 ![]() ,求a和c的值.
,求a和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中学校在2015年的一次体能测试中,规定所有男生必须依次参加50米跑、立定跳远和一分钟的引体向上三项测试,只有三项测试全部达标才算合格,已知男生甲的50米跑和立定跳远的测试与男生乙的50米跑测试已达标,男生甲还需要参加一分钟的引体向上测试,男生乙还需要参加立定跳远和一分钟引体向上两项测试,若甲参加一分钟引体向上测试达标的概率为p,乙参加立定跳远和一分钟引体向上的测试达标的概率均为 ![]() ,甲乙每一项测试是否达标互不影响,已知甲和乙同时合格的概率为
,甲乙每一项测试是否达标互不影响,已知甲和乙同时合格的概率为 ![]() .
.
(1)求p的值,并计算甲和乙恰有一人合格的概率;
(2)在三项测试项目中,设甲达标的测试项目项数为x,乙达标的测试项目项数为y,记ξ=x+y,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,准备在墙上钉一个支架,支架由两直杆AC与BD 焊接而成,焊接点 D 把杆AC 分成 AD, CD 两段,其中两固定点A,B 间距离为1 米,AB 与杆 AC 的夹角为60 ,杆AC 长为 1 米,若制作 AD 段的成本为a 元/米,制作 CD 段的成本是 2a 元/米,制作杆BD 成本是 3a 元/米. 设 ADB ,则制作整个支架的总成本记为 S 元.
(1)求S关于 的函数表达式,并求出的取值范围;
(2)问 ![]() 段多长时,S最小?
段多长时,S最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C所对的边分别为a、b、c,已知a≠b,cos2A﹣cos2B= ![]() sinAcosA﹣
sinAcosA﹣ ![]() sinBcosB. (Ⅰ)求角C的大小;
sinBcosB. (Ⅰ)求角C的大小;
(Ⅱ)若c= ![]() ,siniA=
,siniA= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com