��������1��֤��һ������ԭ����Բ�ڣ�Բ��������뷽�̣����̵����С��0��ֱ��֤��F��0��
֤������A��C����ֱ���x�����������ϣ���A��a��0����C��c��0��������ac��0������x
2+y
2+Dx+Ey+F=0����y=0ʱ���ɵ�
x
2+Dx+F=0�����з��̵������ֱ�Ϊ��A�͵�C�ĺ����꣬�Ƴ�x
Ax
C=ac=F���õ����ۣ�
��2���ı���ABCD�����Ϊ8���Խ���AC�ij�Ϊ2����
•=0���õ�|BD|=8���Ƴ�r=4��������D
2+E
2-4F��ֵ��
��3����A��B��C��D�����꣬�����G������Ϊ
(��)����
=(��)��ͨ��AB��OH��֤��G��O��H���㹲�ߣ�ֻ��֤
•=0���ɣ�
����⣺��1��֤��һ�������⣬ԭ��O�ض���ԲM�ڣ����㣨0��0�����뷽��x
2+y
2+Dx+Ey+F=0����ߺ��ֵС��0��
������F��0����֤������4�֣�
֤�����������⣬���ѷ���A��C����ֱ���x�����������ϣ�����������ֱ�Ϊ
A��a��0����C��c��0��������ac��0��
����Բ����x
2+y
2+Dx+Ey+F=0����y=0ʱ���ɵ�x
2+Dx+F=0�����з��̵������ֱ�Ϊ��A�͵�C�ĺ����꣬������x
Ax
C=ac=F��
��Ϊac��0����F��0������4�֣�
��2�����ѷ��֣��Խ����ഹֱ���ı���ABCD���S=
����ΪS=8��|AC|=2���ɵ�|BD|=8������6�֣�
����Ϊ
•=0�����ԡ�AΪֱ�ǣ�����Ϊ�ı�����ԲM���ڽ��ı��Σ���|BD|=2r=8⇒r=4������8�֣�
���ڷ���x
2+y
2+Dx+Ey+F=0����ʾ��Բ����֪
+-F=r2������D
2+E
2-4F=4r
2=64������10�֣�
��3��֤�����ı����ĸ����������ֱ�ΪA��a��0����B��0��b����C��c��0����D��0��d����
��ɵõ�G������Ϊ
(��)����
=(��)������12�֣�
��
=(-A��B)����AB��OH����ҪʹG��O��H���㹲�ߣ�ֻ��֤
•=0���ɣ�
��
•=���Ҷ���ԲM��һ�㷽��x
2+y
2+Dx+Ey+F=0��
��y=0ʱ�ɵ�x
2+Dx+F=0�����з��̵������ֱ�Ϊ��A�͵�C�ĺ����꣬
������x
Ax
C=ac=F������14�֣�
ͬ������x=0ʱ���ɵ�y
2+Ey+F=0�����з��̵������ֱ�Ϊ��B�͵�D�������꣬������y
By
D=bd=F��
���ԣ�
•==0����AB��OG��
��O��G��H�ض����㹲�ߣ�����16�֣�

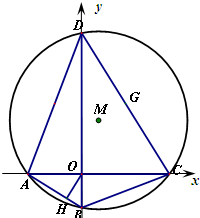 ��ͼ����ƽ��ֱ������ϵ�У�����Ϊx2+y2+Dx+Ey+F=0��ԲM���ڽ��ı���ABCD�ĶԽ���AC��BD���ഹֱ����AC��BD�ֱ���x���y���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�����Ϊx2+y2+Dx+Ey+F=0��ԲM���ڽ��ı���ABCD�ĶԽ���AC��BD���ഹֱ����AC��BD�ֱ���x���y���ϣ�


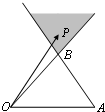 ��ͼ���ڡ�OAB�У���P���߶�OB���߶�AB�ӳ�����Χ�ɵ���Ӱ�����߽磩������һ�㣬��
��ͼ���ڡ�OAB�У���P���߶�OB���߶�AB�ӳ�����Χ�ɵ���Ӱ�����߽磩������һ�㣬�� 1����ͼ����ֱ������ƽ������һ���߳�Ϊa��������ԭ��O����������ABCDEF��AB��Ox��ֱ��L��y=kx+t��kΪ���������������ν���M��N���㣬�ǡ�OMN�����ΪS������S=f��t������ż��Ϊ
1����ͼ����ֱ������ƽ������һ���߳�Ϊa��������ԭ��O����������ABCDEF��AB��Ox��ֱ��L��y=kx+t��kΪ���������������ν���M��N���㣬�ǡ�OMN�����ΪS������S=f��t������ż��Ϊ
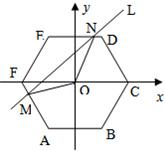 ��ͼ����ֱ������ƽ������һ���߳�Ϊa��������ԭ��O����������ABCDEF��AB��Ox��ֱ��L��y=kx+t��kΪ���������������ν���M��N���㣬�ǡ�OMN�����ΪS������S=f��t������ż��Ϊ��������
��ͼ����ֱ������ƽ������һ���߳�Ϊa��������ԭ��O����������ABCDEF��AB��Ox��ֱ��L��y=kx+t��kΪ���������������ν���M��N���㣬�ǡ�OMN�����ΪS������S=f��t������ż��Ϊ�������� ��2008•������һģ����ͼ����ֱ������ƽ���ڣ�����OT����60����ձ��ϣ�����һ������OA��OA���ڡ�xOT�ڵĸ�����
��2008•������һģ����ͼ����ֱ������ƽ���ڣ�����OT����60����ձ��ϣ�����һ������OA��OA���ڡ�xOT�ڵĸ�����