分析:(1)作CO⊥AA
1交AA
1的延长线于点O,连接BO,则CO⊥平面ABB
1A
1,先证△OAC≌△BAO,则BO⊥AA
1,根据公式cos∠CAB=cos∠OAC•cos∠OAB可求出∠CAB的大小;
(2)以O为坐标原点,OB、OA、OC分别为x、y、z轴,建立空间直角坐标系O-xyz,求出向量
和平面A
1B
1C
1的法向量
,然后根据cos<
,
>=
,从而求出GC
1与平面A
1B
1C
1所成角的大小.
解答:解:作CO⊥AA
1交AA
1的延长线于点O,连接BO,则CO⊥平面ABB
1A
1根据△OAC≌△BAO,所以BO⊥AA
1,
(1)由cos∠CAB=cos∠OAC•cos∠OAB
知cos∠CAB=coa
245°=
∴∠CAB=60°
(2)以O为坐标原点,建立如图所示的空间直角坐标系O-xyz
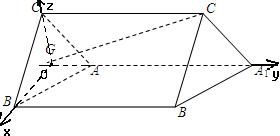
则A(0,1,0),B(1,0,0),C(0,0,1)
∴G(
,
,
),B
1(1,4,0),A
1(0,5,0),C
1(0,4,1)
∴
=(-
,
,
)
设平面A
1B
1C
1的法向量为
=(x,y,z)
由
⇒x=y=z
取n=(1,1,1)
∵cos<
,
>=
==∴GC
1与平面A
1B
1C
1所成角的大小为
-arccos
,即arcsin
.
点评:本题主要考查了用空间向量求直线与平面的夹角,同时考查了计算能力和论证推理的能力,属于中档题.

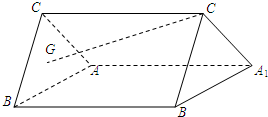 (2008•成都二模)如图,斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,AC=AB=
(2008•成都二模)如图,斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,AC=AB=

