
【题目】边长为![]() 的等边三角形内任一点到三边距离之和为定值,这个定值等于
的等边三角形内任一点到三边距离之和为定值,这个定值等于![]() ;将这个结论推广到空间是:棱长为
;将这个结论推广到空间是:棱长为![]() 的正四面体内任一点到各面距离之和等于________________.(具体数值)
的正四面体内任一点到各面距离之和等于________________.(具体数值)
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所有抽取的30岁以上的网民中利用分层抽样抽取5人,
![]() 求这5人中经常使用、偶尔或不用共享单车的人数;
求这5人中经常使用、偶尔或不用共享单车的人数;
![]() 从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 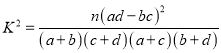 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖一次.抽奖方法是:从装有标号为![]() 的
的![]() 个红球和标号为
个红球和标号为![]() 的
的![]() 个白球的箱中,随机摸出
个白球的箱中,随机摸出![]() 个球,若摸出的两球号码相同,可获一等奖;若两球颜色不同且号码相邻,可获二等奖,其余情况获三等奖.已知某顾客参与抽奖一次.
个球,若摸出的两球号码相同,可获一等奖;若两球颜色不同且号码相邻,可获二等奖,其余情况获三等奖.已知某顾客参与抽奖一次.
(Ⅰ)求该顾客获一等奖的概率;
(Ⅱ)求该顾客获三获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟建一座平面图为矩形,面积为![]() ,高度一定的三段污水处理池(如图),由于受地形限制,其长、宽都不超过
,高度一定的三段污水处理池(如图),由于受地形限制,其长、宽都不超过![]() ,如果池的外壁的建造费单价为
,如果池的外壁的建造费单价为![]() 元
元![]() ,池中两道隔壁墙(与宽边平行)的建造费单价为
,池中两道隔壁墙(与宽边平行)的建造费单价为![]() 元
元![]() ,池底的建造费单价为
,池底的建造费单价为![]() 元
元![]() .设水池的长为
.设水池的长为![]() ,总造价为
,总造价为![]() .
.

(1)求![]() 的表达式;
的表达式;
(2)水池的长与宽各是多少时,总造价最低,并求出这个最低造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com