
【题目】已知椭圆两焦点 ![]() ,并且经过点
,并且经过点 ![]() .
.
(1)求椭圆的方程;
(2)若过点A(0,2)的直线l与椭圆交于不同的两点M、N(M在A、N之间),试求△OAM与△OAN面积之比的取值范围.
【答案】
(1)解:因为椭圆的焦点在x上,
所以设椭圆方程为 ![]() (a>b>0),
(a>b>0),
由定义得 ![]() +,
+,
∴a=2,b2=4﹣3=1,所以椭圆方程为 ![]()
(2)解:由题意知直线l的斜率存在且不为零,设l方程为y=kx+2(k≠0),
设M(x1,y1),N(x2,y2),
由 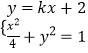 整理得(1+4k2)x2+16kx+12=0,
整理得(1+4k2)x2+16kx+12=0,
由△=256k2﹣48(1+4k2)>0,得 ![]() ;
;
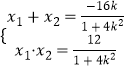 ,
,
令 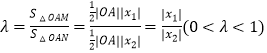 ,
,
∵x1x2>0,∴x1,x2同号,∴ ![]() ∴x1=λx2,
∴x1=λx2,
∴ 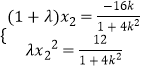 ,
,
∴ 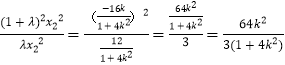
∴ ![]()
∵ ![]() ∴
∴ ![]() ,解得
,解得 ![]() ,
,
∵0<λ<1∴ ![]() ,
,
所以△OAM与△OAN面积之比的取值范围是 ![]()
【解析】(1)设椭圆方程为 ![]() (a>b>0),运用椭圆的定义,可得a=2,结合a,b,c的关系,求得b,进而得到椭圆方程;(2)设l方程为y=kx+2(k≠0),M(x1 , y1),N(x2 , y2),代入椭圆方程,运用判别式大于0和韦达定理,令
(a>b>0),运用椭圆的定义,可得a=2,结合a,b,c的关系,求得b,进而得到椭圆方程;(2)设l方程为y=kx+2(k≠0),M(x1 , y1),N(x2 , y2),代入椭圆方程,运用判别式大于0和韦达定理,令 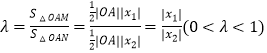 ,代入化简整理,运用不等式的性质,即可得到所求范围.
,代入化简整理,运用不等式的性质,即可得到所求范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知OPQ是半径为 ![]() 圆心角为
圆心角为 ![]() 的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 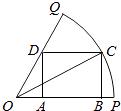
(Ⅰ)若Rt△CBO的周长为 ![]() ,求
,求 ![]() 的值.
的值.
(Ⅱ)求 ![]() 的最大值,并求此时α的值.
的最大值,并求此时α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是 ![]() ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1]
B.[1,7]
C.[7,12]
D.[0,1]和[7,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式:b= 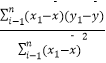 =
= 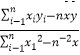 .
.
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x3+3ax2+3bx+8c在x=1及x=2时取得极值. (Ⅰ)求a、b的值;
(Ⅱ)若对任意的x∈[0,3],都有f(x)<c2成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据: ![]() ,
, ![]() ,
,
如果由资料知y对x呈线性相关关系.试求:
(1)![]() ;
;
(2)线性回归方程 ![]() =bx+a.
=bx+a.
(3)估计使用10年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com