
【题目】已知在△ABC中,角A,B,C所对的边分别是a,b,c,且a、b、c成等比数列,c= ![]() bsinC﹣ccosB.
bsinC﹣ccosB.
(Ⅰ)求B的大小;
(Ⅱ)若b=2 ![]() ,求△ABC的周长和面积.
,求△ABC的周长和面积.
【答案】解:(Ⅰ)根据题意,若c= ![]() bsinC﹣ccosB, 由正弦定理可得sinC=
bsinC﹣ccosB, 由正弦定理可得sinC= ![]() sinBsinC﹣sinCcosB,
sinBsinC﹣sinCcosB,
又由sinC≠0,则有1= ![]() sinC﹣cosB,
sinC﹣cosB,
即1=2sin(B﹣ ![]() ),
),
则有B﹣ ![]() =
= ![]() 或B﹣
或B﹣ ![]() =
= ![]() ,即B=
,即B= ![]() 或π(舍)
或π(舍)
故B= ![]() ;
;
(Ⅱ)已知b=2 ![]() ,则b2=a2+c2﹣2accosB=a2+c2﹣ac=(a+c)2﹣3ac=12,
,则b2=a2+c2﹣2accosB=a2+c2﹣ac=(a+c)2﹣3ac=12,
又由a、b、c成等比数列,即b2=ac,
则有12=(a+c)2﹣36,解可得a+c=4 ![]() ,
,
所以△ABC的周长l=a+b+c=2 ![]() +4
+4 ![]() =6
=6 ![]() ,
,
面积S△ABC= ![]() acsinB=
acsinB= ![]() b2sinB=3
b2sinB=3 ![]()
【解析】(Ⅰ)根据题意,由正弦定理可得sinC= ![]() sinBsinC﹣sinCcosB,进而变形可得1=
sinBsinC﹣sinCcosB,进而变形可得1= ![]() sinC﹣cosB,由正弦的和差公式可得1=2sin(B﹣
sinC﹣cosB,由正弦的和差公式可得1=2sin(B﹣ ![]() ),即可得B﹣
),即可得B﹣ ![]() 的值,计算可得B的值,即可得答案;(Ⅱ)由余弦定理可得(a+c)2﹣3ac=12,又由a、b、c成等比数列,进而可以变形为12=(a+c)2﹣36,解可得a+c=4
的值,计算可得B的值,即可得答案;(Ⅱ)由余弦定理可得(a+c)2﹣3ac=12,又由a、b、c成等比数列,进而可以变形为12=(a+c)2﹣36,解可得a+c=4 ![]() ,进而计算可得△ABC的周长l=a+b+c,由面积公式S△ABC=
,进而计算可得△ABC的周长l=a+b+c,由面积公式S△ABC= ![]() acsinB=
acsinB= ![]() b2sinB计算可得△ABC的面积.
b2sinB计算可得△ABC的面积.
【考点精析】认真审题,首先需要了解正弦定理的定义(正弦定理:![]() ).
).


科目:高中数学 来源: 题型:
【题目】若函数![]() 的图象的相邻两条对称轴之间的距离为
的图象的相邻两条对称轴之间的距离为![]() ,
,![]() ,则下列说法正确的是__________.(写出所有正确结论的序号)
,则下列说法正确的是__________.(写出所有正确结论的序号)
①![]() 是偶函数;
是偶函数;
②函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③函数![]() 在
在![]() 上单调递增;
上单调递增;
④将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,可得函数
个单位长度,可得函数![]() 的图象;
的图象;
⑤![]() 的对称轴方程为
的对称轴方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(![]() sinx+cosx)-
sinx+cosx)-![]() ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)设![]() >0,若函数g(x)=f(x+
>0,若函数g(x)=f(x+![]() )为奇函数,求
)为奇函数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图. 男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
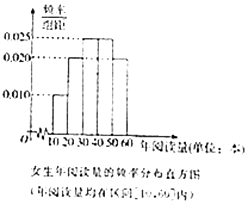
(1)根据女生的频率分布直方图估计该校女生年阅读量的中位数;
(2)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(3)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P(K2≥k0) | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且过点
,且过点 ![]()
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设直线 ![]() 与圆
与圆 ![]() 相切于点
相切于点 ![]() ,且
,且 ![]() 与椭圆
与椭圆 ![]() 只有一个公共点
只有一个公共点 ![]() .
.
①求证: ![]() ;
;
②当 ![]() 为何值时,
为何值时, ![]() 取得最大值?并求出最大值.
取得最大值?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+ ![]() ,其中a>0.
,其中a>0.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)证明:(1+ ![]() )(1+
)(1+ ![]() )(1+
)(1+ ![]() )…(1+
)…(1+ ![]() )<e
)<e ![]() (n∈N* , n≥2).
(n∈N* , n≥2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统综》是明朝程大位所著数学名著,其中有这样一段表述:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一”,其意大致为:有一七层宝塔,每层悬挂的红灯数为上一层的两倍,共有381盏灯,则塔从上至下的第三层有( )盏灯.
A.14
B.12
C.10
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com