
【题目】设![]() ,
,![]() ,
,![]() 表示三条不同的直线,
表示三条不同的直线,![]() ,
,![]() ,
,![]() 表示三个不同的平面,给出下列四个结论:
表示三个不同的平面,给出下列四个结论:
①若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() 是
是![]() 在
在![]() 内的射影,
内的射影,![]() ,则
,则![]() ;
;
③若![]() 是平面
是平面![]() 的一条斜线,
的一条斜线,![]() ,
,![]() 为过
为过![]() 的一条动直线,则可能有
的一条动直线,则可能有![]() 且
且![]() ;
;
④若![]() ,
,![]() ,则
,则![]() .
.
其中正确的个数为( )个.
A.1B.2C.3D.4
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
【题目】要得到函数![]() 的图象,只要将函数
的图象,只要将函数![]() 的图象( )
的图象( )
A.每一点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图象向左平移
倍(纵坐标不变),再将所得图象向左平移![]() 个长度
个长度
B.每一点的横坐标变为原来的![]() 倍(纵坐标不变),再将所得图象向左平移
倍(纵坐标不变),再将所得图象向左平移![]() 个长度
个长度
C.向左平移![]() 个长度,再将所得图象每一点的横坐标变为原来的
个长度,再将所得图象每一点的横坐标变为原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
D.向左平移![]() 个长度,再将所得图象每一点的横坐标变为原来的
个长度,再将所得图象每一点的横坐标变为原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,且
,且![]() )是定义域为R的奇函数.
)是定义域为R的奇函数.
(1)求t的值;
(2)若![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 恒成立的实数k的取值范围;
恒成立的实数k的取值范围;
(3)若函数![]() 的图象过点
的图象过点![]() ,是否存在正数m(
,是否存在正数m(![]() ),使函数
),使函数![]() 在
在![]() 上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
上的最大值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)已知抛物线上一点![]() ,过点
,过点![]() 作抛物线的两条弦
作抛物线的两条弦![]() 和
和![]() ,且
,且![]() ,判断直线
,判断直线![]() 是否过定点?并说明理由.
是否过定点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|ax2+2x+1=0,a∈R},
(1)若A只有一个元素,试求a的值,并求出这个元素;
(2)若A是空集,求a的取值范围;
(3)若A中至多有一个元素,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广州亚运会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向广州亚组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元.(
元.(![]() )
)
(1)写出该专营店一年内销售这种纪念章所获利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出最大值.
(元)最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
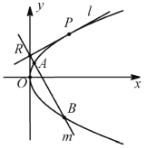
【题目】如图,直线![]() 不与坐标轴垂直,且与抛物线
不与坐标轴垂直,且与抛物线![]() 有且只有一个公共点
有且只有一个公共点![]() .
.
(1)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点.当
两点.当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com