
����Ŀ�����й����ʽ��ڲ�������2018��11��5����10�����Ϻ��Ĺ��һ�չ���ľٰ�.����չ����ҵչ����ó��̳�����²�Ʒ�㼯�����������ߵ�׳�.һ�����ӿ��ź����ŵ��й�������ʵ���ж�Ϊ���繹����ͬ��չƽ̨��չ���ƶ�ȫ��ó����������й�����.
ij�����˾�����˸߶����ܼҾӲ�Ʒ��չ��������Ǣ̸�ɹ�������������Ͷ���й��г�.��֪�ò�Ʒ��̶��з��ɱ�30����Ԫ��ÿ����һ̨����Ͷ��90��Ԫ.��ù�˾һ���������ò�Ʒ![]() ��̨��ȫ�����꣬ÿ��̨����������Ϊ
��̨��ȫ�����꣬ÿ��̨����������Ϊ![]() ����Ԫ,
����Ԫ,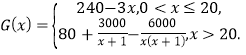
��1��д��������![]() ������Ԫ�����������
������Ԫ�����������![]() ����̨���ĺ�������ʽ��������=��������-�ɱ���
����̨���ĺ�������ʽ��������=��������-�ɱ���
��2���������Ϊ������̨ʱ���ù�˾��õ������������������.
���𰸡���1��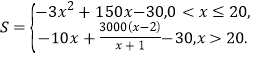 ����2���������Ϊ29��̨ʱ���ù�˾�ڸò�Ʒ�л�õ���������������Ϊ2380��Ԫ.
����2���������Ϊ29��̨ʱ���ù�˾�ڸò�Ʒ�л�õ���������������Ϊ2380��Ԫ.
��������
��1����![]() ���Ե��ۣ���ȥÿ̨��Ͷ��ɱ��Լ��̶��ɱ����ɴ�����������������ı���ʽ.��2�����ö��κ�������ֵ�ͻ�������ʽ����ò���Ϊ����ʱ�������������.
���Ե��ۣ���ȥÿ̨��Ͷ��ɱ��Լ��̶��ɱ����ɴ�����������������ı���ʽ.��2�����ö��κ�������ֵ�ͻ�������ʽ����ò���Ϊ����ʱ�������������.
��1����![]() ʱ��
ʱ��![]()
![]() ��
��
��![]() ʱ��
ʱ��![]()
![]() .
.
��������ʽΪ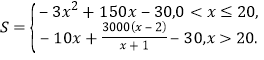
��2����![]() ʱ����Ϊ
ʱ����Ϊ![]() ��
��![]() ��
��![]() �ϵ���������
�ϵ���������
���Ե�![]() ʱ��
ʱ��![]() .
.
��![]() ʱ��
ʱ��![]()
![]()
![]()
![]() .
.
���ҽ���![]() ����
����![]() ʱ�Ⱥų���.
ʱ�Ⱥų���.
��Ϊ![]() ������
������![]() ʱ��
ʱ��![]() �����ֵΪ2380����Ԫ.
�����ֵΪ2380����Ԫ.
�𣺵������Ϊ29��̨ʱ���ù�˾�ڸò�Ʒ�л�õ���������������Ϊ2380��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
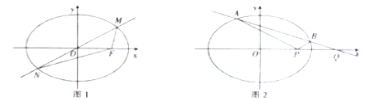
����Ŀ����ͼ����֪��Բ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ����
����![]() ����Բ
����Բ![]() �ϣ���ԭ��
�ϣ���ԭ��![]() ��ֱ������Բ
��ֱ������Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() .
.
��������Բ![]() �ķ��̣�
�ķ��̣�
������![]() ��
��![]() ������
������![]() ��б�ʲ�Ϊ���ֱ������Բ
��б�ʲ�Ϊ���ֱ������Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬֤����
���㣬֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
(��)��![]() ʱ��������
ʱ��������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
(��)��![]() ʱ����
ʱ����![]() ������
������![]() �ϵ���СֵΪ-2������
�ϵ���СֵΪ-2������![]() ����Ȼ�����ĵ�������ʵ��
����Ȼ�����ĵ�������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��ex��e��x��g(x)��2x��ax3��aΪʵ������
(1)��g(x)�ĵ������䣻
(2)��a����1ʱ��֤��������x0��(0��1)��ʹ��y��f(x)��y��g(x)��ͼ����x��x0����������ƽ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2021��㶫�¸߿���ʵ����![]() ��ģʽ�������ġ���ѧ��Ӣ���ѡ����������ʷ��ѡһ�����Ρ���������ѧ��������ѡ������ѡ���ƲμӸ߿�.����ƫ�������Ƕ�ѡһʱѡ������ƫ�ķ����Ƕ�ѡһʱѡ��ʷ���Ժ��Ŀ�ѡ��û����.
��ģʽ�������ġ���ѧ��Ӣ���ѡ����������ʷ��ѡһ�����Ρ���������ѧ��������ѡ������ѡ���ƲμӸ߿�.����ƫ�������Ƕ�ѡһʱѡ������ƫ�ķ����Ƕ�ѡһʱѡ��ʷ���Ժ��Ŀ�ѡ��û����.
��1��С�����ѡ�Σ�����ѡ��ƫ����������ѧ�Ƶĸ��ʣ�
��2��С����С��ͬʱ���ѡ�Σ�Լ��ѡ��ƫ����������ѧ�ƣ�������ѡ����ͬ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ס�������������С�����ڵIJ����̶ȣ������������飺��200ֻС������ֳ�![]() ���飬ÿ��100ֻ������
���飬ÿ��100ֻ������![]() ��С�������������Һ��
��С�������������Һ��![]() ��С�������������Һ.ÿֻС���������Һ�����ͬ��Ħ��Ũ����ͬ.����һ��ʱ�����ij�ֿ�ѧ���������������С���������ӵİٷֱ�.�����������ݷֱ�õ�����ֱ��ͼ��
��С�������������Һ.ÿֻС���������Һ�����ͬ��Ħ��Ũ����ͬ.����һ��ʱ�����ij�ֿ�ѧ���������������С���������ӵİٷֱ�.�����������ݷֱ�õ�����ֱ��ͼ��

��![]() Ϊ�¼����������Ӳ��������ڵİٷֱȲ�����
Ϊ�¼����������Ӳ��������ڵİٷֱȲ�����![]() ��������ֱ��ͼ�õ�
��������ֱ��ͼ�õ�![]() �Ĺ���ֵΪ
�Ĺ���ֵΪ![]() .
.
��1���������Ӳ����ٷֱ�ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2���ֱ���Ƽס������Ӳ����ٷֱȵ�ƽ��ֵ��ͬһ���е������ø���������е�ֵΪ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�����C�IJ�������Ϊ![]() ������Ϊ����������ԭ��Ϊ���㣬x��Ǹ�����Ϊ���Ὠ��������ϵ��
������Ϊ����������ԭ��Ϊ���㣬x��Ǹ�����Ϊ���Ὠ��������ϵ��
��1��������C�ļ����귽�̣�
��2����ƽ��ֱ������ϵxOy�У�A����2��0����B��0����2����M������C������һ�㣬����ABM�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����μ�����Ӫ��400��ѧ�����Ϊ��001��002������400������ϵͳ�����ķ�����ȡһ������Ϊ40���������������õĺ���Ϊ003����400��ѧ����ס������Ӫ������001��180�ڵ�һӪ������181��295�ڵڶ�Ӫ������296��400�ڵ���Ӫ��������Ӫ�������е������ֱ�Ϊ( )
A. 18��12��10 B. 20��12��8 C. 17��13��10 D. 18��11��11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й����ƾõĽ�ʯ�Ļ���ӡ���ǽ�ʯ�Ļ��Ĵ���֮һ��ӡ�ŵ���״��Ϊ�����塢�������Բ���壬���ϱ���ʱ�ڵĹ�Ա�����ŵ�ӡ����״������������������ͼ1��.�����������������ֻ��������ϵ��������Χ�ɵĶ�����.������������������ѧ�ĶԳ�����ͼ2��һ������Ϊ48�İ��������壬�������ж��㶼��ͬһ��������ı����ϣ��Ҵ���������ⳤΪ1����ð��������干��________���棬���ⳤΪ_________��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com