
【题目】某地实施乡村振兴战略,对农副产品进行深加工以提高产品附加值,已知某农产品成本为每件3元,加工后的试营销期间,对该产品的价格与销售量统计得到如下数据:
单价x(元) | 6 | 6.2 | 6.4 | 6.6 | 6.8 | 7 |
销量y(万件) | 80 | 74 | 73 | 70 | 65 | 58 |
数据显示单价x与对应的销量y满足线性相关关系.
(1)求销量y(件)关于单价x(元)的线性回归方程![]() ;
;
(2)根据销量y关于单价x的线性回归方程,要使加工后收益P最大,应将单价定为多少元?(产品收益=销售收入-成本).
参考公式:![]() =
= =
= ,
,![]()
科目:高中数学 来源: 题型:
【题目】已知动点M到定点F1(-2,0)和F2(2,0)的距离之和为![]() .
.
(1)求动点M轨迹C的方程;
(2)设N(0,2),过点P(-1,-2)作直线l,交椭圆C于不同于N的A,B两点,直线NA,NB的斜率分别为k1,k2,问k1+k2是否为定值?若是的求出这个值.
查看答案和解析>>
科目:高中数学 来源: 题型:
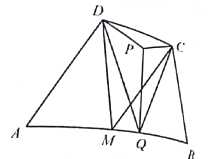
【题目】如图,在凸四边形ABCD中,M为边AB的中点,且MC=MD.分别过点C、D作边BC、AD的垂线,设两条垂线的交点为P.过点P作![]() 与Q.求证:
与Q.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网络外卖也开始成为不少人日常生活中不可或缺的一部分![]() 市某调查机构针对该市市场占有率最高的两种网络外卖企业
市某调查机构针对该市市场占有率最高的两种网络外卖企业![]() 以下简称外卖A、外卖
以下简称外卖A、外卖![]() 的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
的服务质量进行了调查,从使用过这两种外卖服务的市民中随机抽取了1000人,每人分别对这两家外卖企业评分,满分均为100分,并将分数分成5组,得到以下频数分布表:
分数 人数 种类 |
|
|
|
|
|
外卖A | 50 | 150 | 100 | 400 | 300 |
外卖B | 100 | 100 | 300 | 200 | 300 |
表中得分越高,说明市民对网络外卖服务越满意![]() 若得分不低于60分,则表明该市民对网络外卖服务质量评价较高
若得分不低于60分,则表明该市民对网络外卖服务质量评价较高![]() 现将分数按“服务质量指标”划分成以下四个档次:
现将分数按“服务质量指标”划分成以下四个档次:
分数 |
|
|
|
|
服务质量指标 | 0 | 1 | 2 | 3 |
视频率为概率,解决下列问题:
![]() 从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
从该市使用过外卖A的市民中任选5人,记对外卖A服务质量评价较高的人数为X,求X的数学期望.
![]() 从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
从参与调查的市民中随机抽取1人,试求其评分中外卖A的“服务质量指标”与外卖B的“服务质量指标”的差的绝对值等于2的概率;
![]() 在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
在M市工作的小王决定从外卖A、外卖B这两种网络外卖中选择一种长期使用,如果从这两种外卖的“服务质量指标”的期望角度看,他选择哪种外卖更合适?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,定义椭圆
,定义椭圆![]() 的“相关圆”方程为
的“相关圆”方程为![]() .若抛物线
.若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的一个焦点重合,且椭圆
的一个焦点重合,且椭圆![]() 短轴的一个端点和其两个焦点构成直角三角形.
短轴的一个端点和其两个焦点构成直角三角形.
(1)求椭圆![]() 的方程和“相关圆”
的方程和“相关圆”![]() 的方程;
的方程;
(2)过“相关圆”![]() 上任意一点
上任意一点![]() 的直线l:
的直线l:![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.O为坐标原点,若
两点.O为坐标原点,若![]() ,证明原点O到直线
,证明原点O到直线![]() 的距离是定值,并求
的距离是定值,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线的一条弦的中点作平行于抛物线对称轴的平行线(或与对称轴重合),交抛物线于一点,称以该点及弦的端点为顶点的三角形为这条弦的阿基米德三角形(简称阿氏三角形).
现有抛物线![]() :
:![]() ,直线
,直线![]() :
:![]() (其中
(其中![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() ),直线
),直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,设弦
两点,设弦![]() 的阿氏三角形是
的阿氏三角形是![]() .
.

(1)指出抛物线![]() 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(2)求![]() 的面积(用
的面积(用![]() ,
,![]() ,
,![]() 表示);
表示);
(3)称![]() 的阿氏
的阿氏![]() 为一阶的;
为一阶的;![]() 、
、![]() 的阿氏
的阿氏![]() 、
、![]() 为二阶的;
为二阶的;![]() 、
、![]() 、
、![]() 、
、![]() 的阿氏三角形为三阶的;……,由此进行下去,记所有的
的阿氏三角形为三阶的;……,由此进行下去,记所有的![]() 阶阿氏三角形的面积之和为
阶阿氏三角形的面积之和为![]() ,探索
,探索![]() 与
与![]() 之间的关系,并求
之间的关系,并求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com