
【题目】已知函数![]() (
(![]() ,
,![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当时
的图象.当时![]() ,求函数
,求函数![]() 的值域.
的值域.
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为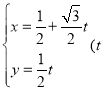 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.

图一

图二
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①A=![]() 的子集有
的子集有![]() 个;
个;
②命题“![]() ”的否定是“
”的否定是“![]() 使得
使得![]() ”;
”;
③“![]() ”是“函数
”是“函数![]() 取得最大值”的充分不必要条件;
取得最大值”的充分不必要条件;
④根据对数定义,对数式![]() 化为指数式
化为指数式![]() ;
;
⑤若![]() ,则
,则![]() 的取值范围为
的取值范围为![]() ;
;
⑥![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
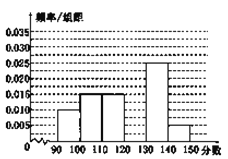
(1)求分数在[120,130)内的频率;
(2)估计本次考试的中位数;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在![]() 上的函数
上的函数![]() 、
、![]() 和
和![]() ,满足
,满足![]() ,且对任意实数
,且对任意实数![]() 、
、![]() (
(![]() ),恒有
),恒有![]() 成立.
成立.
⑴试写 出一组满足条件的具体的![]() 和
和![]() ,使
,使![]() 为增函数,
为增函数,![]() 为减函数,但
为减函数,但![]() 为增函数.
为增函数.
⑵判断下列两个命题的真假,并说明理由.
命题1):若![]() 为增函数,则
为增函数,则![]() 为增函数;
为增函数;
命题2):若![]() 为增函数,则
为增函数,则![]() 为增函数.
为增函数.
⑶已知![]() ,写出一组满足条件的具体的
,写出一组满足条件的具体的![]() 和
和![]() ,且
,且![]() 为非常值函数,并说明理由.
为非常值函数,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com