
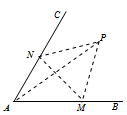
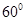 .由正弦定理可得到AM的表达式,在三角形AMP中利用余弦定理表示出AP的值,由角θ的取值范围,再根据三角函数的单调性知识即可得到结论.本小题用了五种解法分别从三角,坐标系,圆等方面入手.
.由正弦定理可得到AM的表达式,在三角形AMP中利用余弦定理表示出AP的值,由角θ的取值范围,再根据三角函数的单调性知识即可得到结论.本小题用了五种解法分别从三角,坐标系,圆等方面入手.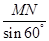 =
=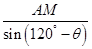 .
.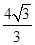 sin(120°-θ). 2分
sin(120°-θ). 2分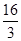 sin2(120°-θ)+4-2×2×
sin2(120°-θ)+4-2×2×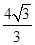 sin(120°θ)cos(60°+θ) 6分
sin(120°θ)cos(60°+θ) 6分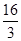 sin2(θ+60°)-
sin2(θ+60°)-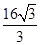 sin(θ+60°)cos(θ+60°)+4
sin(θ+60°)cos(θ+60°)+4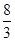 [1-cos (2θ+120°)]-
[1-cos (2θ+120°)]-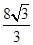 sin(2θ+120°)+4
sin(2θ+120°)+4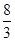 [
[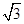 sin(2θ+120°)+cos (2θ+120°)]+
sin(2θ+120°)+cos (2θ+120°)]+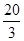
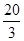 -
-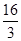 sin(2θ+150°),θ∈(0,120°). 10分
sin(2θ+150°),θ∈(0,120°). 10分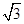 .
.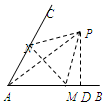
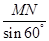 =
=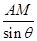 ,
,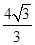 sinθ,∴AD=
sinθ,∴AD=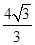 sinθ+2cosθ,(θ≥
sinθ+2cosθ,(θ≥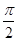 时,结论也正确). 4分
时,结论也正确). 4分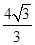 sinθ+2cosθ)2+(2sinθ)2
sinθ+2cosθ)2+(2sinθ)2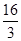 sin2θ+
sin2θ+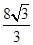 sinθcosθ+4cos2θ+4sin2θ 6分
sinθcosθ+4cos2θ+4sin2θ 6分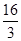 ·
·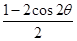 +
+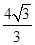 sin2θ+4=
sin2θ+4=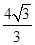 sin2θ-
sin2θ-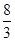 cos2θ+
cos2θ+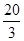
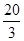 +
+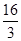 sin(2θ-
sin(2θ-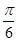 ),θ∈(0,
),θ∈(0,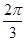 ). 10分
). 10分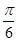 =
=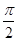 ,即θ=
,即θ=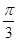 时,AP2取得最大值12,即AP取得最大值2
时,AP2取得最大值12,即AP取得最大值2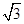 .
.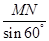 =
=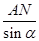 ,即
,即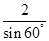 =
=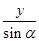 ,
,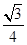 y,cosα=
y,cosα= =
=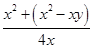 =
=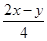 . 4分
. 4分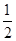 cosα-
cosα-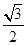 sinα=
sinα=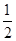 ·
·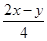 -
-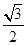 ·
·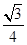 y=
y=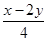 . 6分
. 6分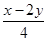 =x2+4-x(x-2y)=4+2xy. 10分
=x2+4-x(x-2y)=4+2xy. 10分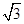 .
.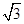 .
. 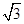 x2),P(x0,y0).∵MN=2,
x2),P(x0,y0).∵MN=2,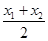 ,
,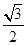 x2).
x2).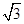 ,PK⊥MN,
,PK⊥MN,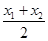 )2+(y0-
)2+(y0-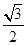 x2)2=3,
x2)2=3,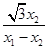 ·
·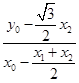 =-1, 4分
=-1, 4分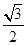 x2=
x2=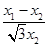 (x0-
(x0-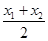 ),∴(y0-
),∴(y0-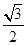 x2)2=
x2)2=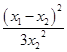 (x0-
(x0-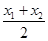 )2
)2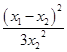 )(x0-
)(x0-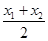 )2=3,即
)2=3,即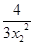 (x0-
(x0-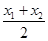 )2=3,∴(x0-
)2=3,∴(x0-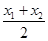 )2=
)2=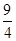 x22.
x22.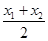 >0 ∴x0-
>0 ∴x0-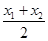 =
=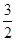 x2,
x2,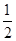 x1+2x2,∴y0=
x1+2x2,∴y0=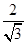 x1. 6分
x1. 6分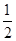 x1)2+
x1)2+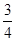 x12=x12+4x22+2x1x2
x12=x12+4x22+2x1x2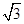 .
. 
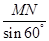 =2R,
=2R,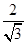 , 8分
, 8分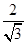 ,又PM=PN,∴PF是线段MN的垂直平分线.
,又PM=PN,∴PF是线段MN的垂直平分线.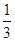 .
.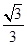 ,又PE=
,又PE=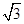 . 10
. 10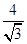 ,∴AP的最大值为PF+R=2
,∴AP的最大值为PF+R=2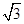 .
. 

科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
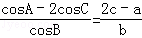 .
.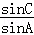 的值;
的值;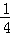 ,△ABC的周长为5,求b的长.
,△ABC的周长为5,求b的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com