
【题目】已知以点![]() 为圆心的圆过点
为圆心的圆过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() ,且
,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)求圆![]() 的方程;
的方程;
(3)是否存在点![]() 在圆
在圆![]() 上,使得
上,使得![]() 的面积为
的面积为![]() ?若存在,请指出共有几个这样的点?说明理由,并求出这些点的坐标.
?若存在,请指出共有几个这样的点?说明理由,并求出这些点的坐标.
【答案】(1) ![]() (2)
(2)![]() 或
或![]() ;(3)存在,有两个点
;(3)存在,有两个点![]() ,当
,当![]() 时,
时,![]() 点坐标为
点坐标为![]() 或
或![]() ;当
;当![]() 时,
时,![]() 点坐标为
点坐标为![]() 或
或![]()
【解析】
(1)由题意知直线![]() 垂直平分线段
垂直平分线段![]() ,由
,由![]() 的坐标求得
的坐标求得![]() 所在直线的斜率,可得
所在直线的斜率,可得![]() 所在直线的斜率,再由中点坐标公式求得
所在直线的斜率,再由中点坐标公式求得![]() 中点坐标,代入直线点斜式方程即得答案;
中点坐标,代入直线点斜式方程即得答案;
(2)由题意知线段![]() 为圆的直径,可得
为圆的直径,可得![]() .设圆P的方程为
.设圆P的方程为![]() ,把
,把![]() 的坐标代入圆的方程,联立求得
的坐标代入圆的方程,联立求得![]() 的值,即可求得圆的方程;
的值,即可求得圆的方程;
(3)由![]() ,当
,当![]() 的面积为
的面积为![]() 时,则点
时,则点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,又因为圆心到直线
,又因为圆心到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,可知圆上共有两个点
,可知圆上共有两个点![]() 满足条件,通过求出的平行直线和圆联立即可求出点
满足条件,通过求出的平行直线和圆联立即可求出点![]() 坐标.
坐标.
(1)由题意知直线![]() 垂直平分线段
垂直平分线段![]() ,
,
![]()
![]()
![]() 中点坐标
中点坐标![]() ,又
,又![]() ,
,![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() ;
;
(2)由题意知线段![]() 为圆的直径,
为圆的直径,
![]()
设圆P的方程为![]() ,
,
∵圆经过点![]() ,
,
 ,
,
解得![]() 或
或![]() .
.
∴圆![]() 的方程为
的方程为![]() 或
或![]() .
.


(3)![]() ,当
,当![]() 的面积为
的面积为![]() 时,点
时,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,又因为圆心到直线
,又因为圆心到直线![]() 的距离为
的距离为![]() ,圆
,圆![]() 的半径为
的半径为![]() ,且
,且![]() ,
,
![]() 圆上共有两个点
圆上共有两个点![]() ,使
,使![]() 的面积为18.
的面积为18.
![]() 点
点![]() 在与直线
在与直线![]() 平行且距离直线
平行且距离直线![]() 的为
的为![]() 的直线
的直线![]() 上,同时圆心
上,同时圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() .直线
.直线![]() 与圆
与圆![]() 的交点即为所求点
的交点即为所求点![]() .
.
当![]() 时,可求得直线
时,可求得直线![]()

![]() 或
或![]() ,所以此时
,所以此时![]() 点坐标为
点坐标为![]() 或
或![]() ;
;
当![]() 时,可求得直线
时,可求得直线![]()

![]() 或
或![]() ,所以此时
,所以此时![]() 点坐标为
点坐标为![]() 或
或![]() ;
;


科目:高中数学 来源: 题型:
【题目】某市10000名职业中学高三学生参加了一项综合技能测试,从中随机抽取100名学生的测试成绩,制作了以下的测试成绩![]() (满分是184分)的频率分布直方图.
(满分是184分)的频率分布直方图.
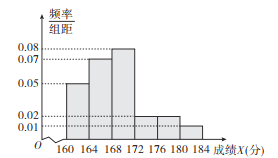
市教育局规定每个学生需要缴考试费100元.某企业根据这100000名职业中学高三学生综合技能测试成绩来招聘员工,划定的招聘录取分数线为172分,且补助已经被录取的学生每个人![]() 元的交通和餐补费.
元的交通和餐补费.
(1)已知甲、乙两名学生的测试成绩分别为168分和170分,求技能测试成绩![]() 的中位数,并对甲、乙的成绩作出客观的评价;
的中位数,并对甲、乙的成绩作出客观的评价;
(2)令![]() 表示每个学生的交费或获得交通和餐补费的代数和,把
表示每个学生的交费或获得交通和餐补费的代数和,把![]() 用
用![]() 的函数来表示,并根据频率分布直方图估计
的函数来表示,并根据频率分布直方图估计![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】问:有多少种不同的方法将集合![]() 中的元素归入
中的元素归入![]() 三个(有序)集合,使得每个元素至少含于其中一个集合之中,这三个集合的交是空集,而其中任两个集合的交都不是空集?
三个(有序)集合,使得每个元素至少含于其中一个集合之中,这三个集合的交是空集,而其中任两个集合的交都不是空集?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了选拔学生参加“全国高中数学联赛”,先在本校进行初赛(满分150分),随机抽取100名学生的成绩作为样本,并根据他们的初赛成绩得到如图所示的频率分布直方图.

(1)求频率分布直方图中a的值;
(2)根据频率分布直方图,估计这次初赛成绩的平均数、中位数、众数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 y = x3 + x-2 在点 P0 处的切线![]() 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线![]() , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com