
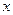 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线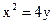 的焦点,离心率
的焦点,离心率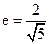 ,过椭圆的右焦点
,过椭圆的右焦点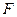 作不与坐标轴垂直的直线
作不与坐标轴垂直的直线 ,交椭圆于A、B两点.
,交椭圆于A、B两点.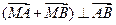 ,求
,求 取值范围;
取值范围;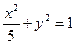
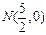
 ,由题意知
,由题意知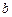 =1.
=1.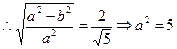 ,
,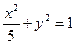 .
. 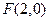 ,所以
,所以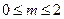 . 设
. 设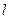 的方程为
的方程为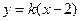
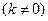 ,
,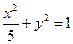 ,得
,得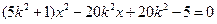 ,
,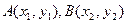 ,则
,则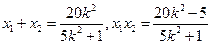 ,
, 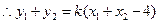 ,
,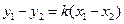 ,
,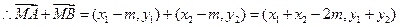 ,
,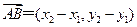 ,
,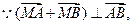
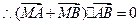 ,
,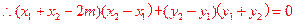 ,
,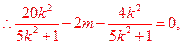
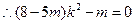 ,
,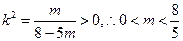 ,
,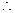 当
当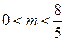 时, 有
时, 有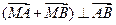 成立.
成立. 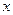 轴上存在定点
轴上存在定点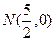 ,使得
,使得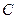 、
、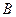 、
、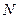 三点共线.
三点共线.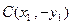 ,直线BC的方程为
,直线BC的方程为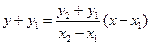 ,
,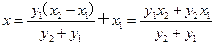 ,
, 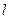 的方程为
的方程为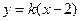 ,A、B在直线
,A、B在直线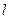 上,
上,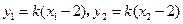
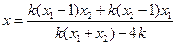
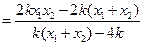
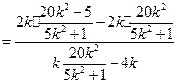
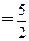
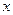 轴上存在定点
轴上存在定点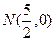 ,使得
,使得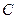 、
、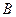 、
、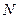 三点共线.
三点共线. 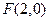 ,所以
,所以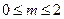 .
. 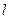 的方程为
的方程为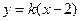
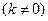 ,
,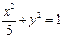 ,得
,得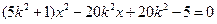 ,
,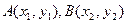 ,则
,则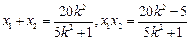 ,
, 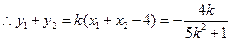 ,
,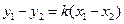 ,
,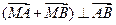 ,∴
,∴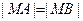 ,
,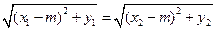 ,
,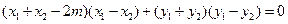 ,
,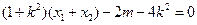 ,∴
,∴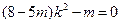 ,
, ∵
∵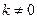 , ∴
, ∴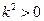 ,
,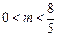 .
.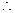 当
当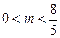 时, , 有
时, , 有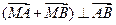 成立.
成立. 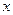 轴上存在定点
轴上存在定点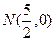 ,使得
,使得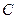 、
、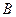 、
、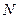 三点共线.
三点共线.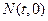 ,使得
,使得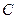 、
、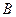 、
、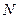 三点共线, 则
三点共线, 则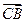 ∥
∥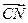 ,
,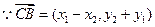 ,
,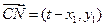 ,
,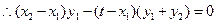 ,
,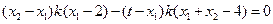 .
.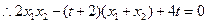
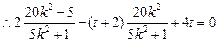 ,
,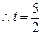 .∴,存在
.∴,存在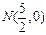 ,使
,使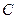 、
、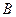 、
、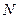 三点共线.
三点共线.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源:不详 题型:解答题
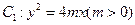 的准线与
的准线与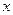 轴交于
轴交于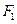 ,焦点为
,焦点为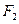 ;以
;以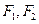 为焦点,离心率
为焦点,离心率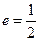 的椭圆
的椭圆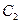 与抛物线
与抛物线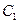 在
在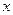 轴上方的交点为
轴上方的交点为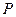 ,延长
,延长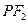 交抛物线于点
交抛物线于点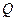 ,
,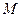 是抛物线
是抛物线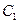 上一动点,且M在
上一动点,且M在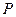 与
与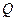 之间运动.
之间运动.
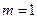 时,求椭圆
时,求椭圆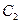 的方程;
的方程;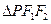 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求 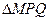 面积的最大值.
面积的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
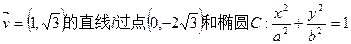
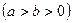 的右焦点,且椭圆的离心率为
的右焦点,且椭圆的离心率为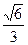 .
.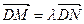 ,求实数
,求实数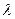 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com