
°Њћвƒњ°њќ“єъ–¬–ЌєЏ„і≤°ґЊЈќ—„“я«й∆ЏЉд£ђ“‘Ќш¬зєЇќпЇЌЌш…ѕЈюќсЋщіъ±нµƒ–¬–ЋѕыЈ—’єѕ÷≥цЅЋ«њіуµƒ…ъ√ьЅ¶£ђ–¬–ЋѕыЈ—љЂ≥…ќ™ќ“єъѕыЈ—‘ц≥§µƒ–¬ґѓƒ№.ƒ≥ –ќ™ЅЋЅЋљв±ЊµЎЊ”√с‘Џ2020ƒк2‘¬÷Ѕ3‘¬ЅљЄц‘¬Ќш¬зєЇќпѕыЈ—«йњц£ђ‘ЏЌш…ѕЋжїъґ‘1000»Ћ„цЅЋќ Њнµч≤й£ђµ√»зѕ¬∆µ эЈ÷≤Љ±н£Ї
ЌшєЇѕыЈ—«йњц£®‘™£© |
|
|
|
|
|
∆µ э | 300 | 400 | 180 | 60 | 60 |
£®1£©„ч≥ц’в–© эЊЁµƒ∆µ¬ Ј÷≤Љ÷±ЈљЌЉ£ђ≤ҐєјЉ∆±Њ –Њ”√сіЋ∆ЏЉдЌш¬зєЇќпµƒѕыЈ—∆љЊщ÷µ£ї
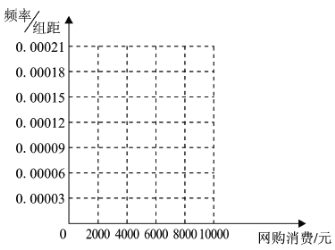
£®2£©‘Џµч≤йќ Њн÷–”–“їѕо «ћо–і±Њ»ЋƒкЅд£ђќ™—–ЊњЌшєЇљрґоЇЌЌшєЇ»ЋƒкЅдµƒєЎѕµ£ђ“‘ЌшєЇљрґо «Јс≥ђєэ4000‘™ќ™±к„Љљш––Ј÷≤г≥й—щ£ђі”…ѕ ц1000»Ћ÷–≥й»°200»Ћ£ђµ√µљ»зѕ¬Ѕ–Ѕ™±н£ђ«лљЂ±н≤є≥дЌк’ы≤ҐЄщЊЁЅ–Ѕ™±н≈–ґѕ£ђ‘ЏіЋ∆ЏЉд «Јс”–95%µƒ∞—ќ’»ѕќ™ЌшєЇљрґо”лЌшєЇ»ЋƒкЅд”–єЎ.
ЌшєЇ≤ї≥ђєэ4000‘™ | ЌшєЇ≥ђєэ4000‘™ | „№Љ∆ | |
40Ћк“‘…ѕ | 75 | 100 | |
40Ћк“‘ѕ¬£®Їђ40Ћк£© | |||
„№Љ∆ | 200 |
≤ќњЉєЂ љЇЌ эЊЁ£Ї![]() .£®∆д÷–
.£®∆д÷–![]() ќ™—щ±Њ»ЁЅњ£©
ќ™—щ±Њ»ЁЅњ£©
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
°Њір∞Є°њ£®1£©„чЌЉЉыљвќц£їєјЉ∆±Њ –Њ”√сіЋ∆ЏЉдЌш¬зєЇќпµƒѕыЈ—∆љЊщ÷µќ™![]() £®‘™£©
£®‘™£©
£®2£©ћо±нЉыљвќц£ї‘ЏіЋ∆ЏЉд√ї”–95%µƒ∞—ќ’»ѕќ™ЌшєЇљрґо”лЌшєЇ»ЋƒкЅд”–єЎ
°Њљвќц°њ
£®1£©Љ∆Ћг≥ц√њ„йµƒ∆µ¬ /„йЊа£ђі”ґшµ√≥ц∆µ¬ Ј÷≤Љ÷±ЈљЌЉ£ђ‘ўЉ∆Ћг∆љЊщ÷µЉіњ…£ї
£®2£©ЄщЊЁЈ÷≤г≥й—щµƒ–‘÷ µ√≥цЌш¬зєЇќпѕыЈ—≤ї≥ђєэ4000‘™ЇЌ≥ђєэ4000‘™≥й»°µƒ»Ћ э£ђћо–іЅ–Ѕ™±н£ђЉ∆Ћг![]() £ђЉіњ…„ч≥ц≈–ґѕ.
£ђЉіњ…„ч≥ц≈–ґѕ.
£®1£©![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]()
‘т![]() ґ‘”¶µƒ∆µ¬ /„йЊаЈ÷±рќ™
ґ‘”¶µƒ∆µ¬ /„йЊаЈ÷±рќ™![]()
і”ґшµ√≥ц∆µ¬ Ј÷≤Љ÷±ЈљЌЉ
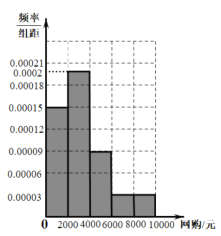
”…∆µ¬ Ј÷≤Љ÷±ЈљЌЉ£ђєјЉ∆±Њ –Њ”√сіЋ∆ЏЉдЌш¬зєЇќпµƒѕыЈ—∆љЊщ÷µќ™![]()
![]() £®‘™£©
£®‘™£©
£®1£©”… эЊЁњ…÷™Ќш¬зєЇќпѕыЈ—≤ї≥ђєэ4000‘™µƒ”–![]() »Ћ
»Ћ
Ќш¬зєЇќпѕыЈ—≥ђєэ4000‘™µƒ”–![]() »Ћ£ђЌк≥…ѕ¬±н£Ї
»Ћ£ђЌк≥…ѕ¬±н£Ї
ЌшєЇ≤ї≥ђєэ4000‘™ | ЌшєЇ≥ђєэ4000‘™ | „№Љ∆ | |
40Ћк“‘…ѕ | 75 | 25 | 100 |
40Ћк“‘ѕ¬£®Їђ40Ћк£© | 65 | 35 | 100 |
„№Љ∆ | 140 | 60 | 200 |
”…єЂ љ![]()
Ћщ“‘‘ЏіЋ∆ЏЉд√ї”–95%µƒ∞—ќ’»ѕќ™ЌшєЇљрґо”лЌшєЇ»ЋƒкЅд”–єЎ.



| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»ф эЅ–![]() ¬ъ„гn°Ё2 ±£ђ
¬ъ„гn°Ё2 ±£ђ![]() £ђ‘т≥∆ эЅ–
£ђ‘т≥∆ эЅ–![]() (n
(n![]() )ќ™
)ќ™![]() µƒ°∞L эЅ–°±£Ѓ
µƒ°∞L эЅ–°±£Ѓ
£®1£©»ф![]() £ђ«“
£ђ«“![]() µƒ°∞L эЅ–°±ќ™
µƒ°∞L эЅ–°±ќ™![]() £ђ«у эЅ–
£ђ«у эЅ–![]() µƒЌ®ѕоєЂ љ£ї
µƒЌ®ѕоєЂ љ£ї
£®2£©»ф![]() £ђ«“
£ђ«“![]() µƒ°∞L эЅ–°±ќ™µЁ‘ц эЅ–£ђ«уkµƒ»°÷µЈґќІ£ї
µƒ°∞L эЅ–°±ќ™µЁ‘ц эЅ–£ђ«уkµƒ»°÷µЈґќІ£ї
£®3£©»ф![]() £ђ∆д÷–p£Њ1£ђЉ«
£ђ∆д÷–p£Њ1£ђЉ«![]() µƒ°∞L эЅ–°±µƒ«∞nѕоЇЌќ™
µƒ°∞L эЅ–°±µƒ«∞nѕоЇЌќ™![]() £ђ ‘≈–ґѕ «Јсіж‘Џµ»≤о эЅ–
£ђ ‘≈–ґѕ «Јсіж‘Џµ»≤о эЅ–![]() £ђґ‘»ќ“вn
£ђґ‘»ќ“вn![]() £ђґЉ”–
£ђґЉ”–![]() ≥…ЅҐ£ђ≤Ґ÷§√чƒгµƒљб¬џ£Ѓ
≥…ЅҐ£ђ≤Ґ÷§√чƒгµƒљб¬џ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ‘ЏЋƒјв„ґP-ABCD÷–£ђµ„√жABCDќ™÷±љ«ћЁ–ќ£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ«“∆љ√ж
£ђ«“∆љ√ж![]() ∆љ√жABCD.
∆љ√жABCD.
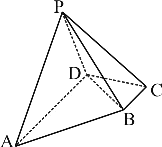
£®1£©«у÷§£Ї![]() £ї
£ї
£®2£©‘ЏѕяґќPA…ѕ «Јсіж‘Џ“їµгM£ђ єґю√жљ«M-BC-Dµƒіу–°ќ™![]() £њ»фіж‘Џ£ђ«у≥ц
£њ»фіж‘Џ£ђ«у≥ц![]() µƒ÷µ£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”….
µƒ÷µ£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”….
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘Џ»эјв÷щ![]() ÷–£ђ“—÷™
÷–£ђ“—÷™![]() «÷±љ«»эљ«–ќ£ђ≤а√ж
«÷±љ«»эљ«–ќ£ђ≤а√ж![]() «ЊЎ–ќ£ђ
«ЊЎ–ќ£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() .
.
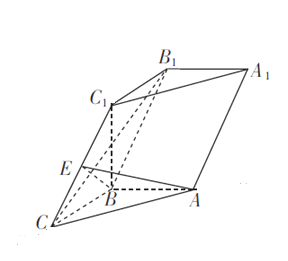
£®1£©÷§√ч£Ї![]() .
.
£®2£©![]() «јв
«јв![]() µƒ÷–µг£ђ«у÷±ѕя
µƒ÷–µг£ђ«у÷±ѕя![]() ”л∆љ√ж
”л∆љ√ж![]() Ћщ≥…љ«µƒ’эѕ“÷µ.
Ћщ≥…љ«µƒ’эѕ“÷µ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њƒ≥÷–—І”–љћ ¶400»Ћ£ђ∆д÷–Єя÷–љћ ¶240»Ћ.ќ™ЅЋЅЋљвЄ√–£љћ ¶√њћмњќЌвґЌЅґ ±Љд£ђѕ÷јы”√Ј÷≤г≥й—щµƒЈљЈ®і”Є√–£љћ ¶÷–Ћжїъ≥й»°ЅЋ100√ыљћ ¶љш––µч≤й£ђЌ≥Љ∆∆д√њћмњќЌвґЌЅґ ±Љд(Ћщ”–љћ ¶√њћмњќЌвґЌЅґ ±ЉдЊщ‘Џ![]() Ј÷÷”ƒЏ)£ђљЂЌ≥Љ∆ эЊЁ∞і
Ј÷÷”ƒЏ)£ђљЂЌ≥Љ∆ эЊЁ∞і![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ°≠£ђ
£ђ°≠£ђ![]() Ј÷≥…6„й£ђ÷∆≥…∆µ¬ Ј÷≤Љ÷±ЈљЌЉ»зѕ¬£Ї
Ј÷≥…6„й£ђ÷∆≥…∆µ¬ Ј÷≤Љ÷±ЈљЌЉ»зѕ¬£Ї
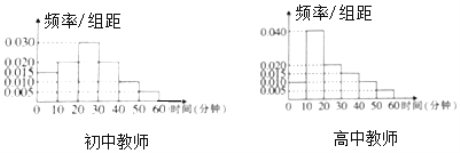
Љў…и√њќїљћ ¶√њћмњќЌвґЌЅґ ±Љдѕаї•ґјЅҐ£ђ≤Ґ≥∆√њћмґЌЅґ ±Љд–°”Џ20Ј÷÷”ќ™»±Ј¶ґЌЅґ.
£®1£© ‘єјЉ∆±Њ–£љћ ¶÷–»±Ј¶ґЌЅґµƒ»Ћ э£ї
£®2£©»фі”≤ќ”лµч≤й£ђ«“√њћмњќЌвґЌЅґ ±Љд‘Џ![]() ƒЏµƒЄ√–£љћ ¶÷–»ќ»°2»Ћ£ђ«у÷Ѕ…ў”–1√ы≥х÷–љћ ¶±ї—°÷–µƒЄ≈¬ .
ƒЏµƒЄ√–£љћ ¶÷–»ќ»°2»Ћ£ђ«у÷Ѕ…ў”–1√ы≥х÷–љћ ¶±ї—°÷–µƒЄ≈¬ .
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ‘Џµ•ќї‘≤O£Їx2+y2£љ1…ѕ»ќ»°“їµгP£®x£ђy£©£ђ‘≤O”лx÷б’эѕтµƒљїµг «A£ђ…иљЂOA»∆‘≠µгO–э„™µљOPЋщ≥…µƒљ«ќ™¶»£ђЉ«x£ђyєЎ”Џ¶»µƒ±ніп љЈ÷±рќ™x£љf£®¶»£©£ђy£љg£®¶»£©£ђ‘тѕ¬Ѕ–ЋµЈ®’э»Јµƒ «£®°°°°£©
A.x£љf£®¶»£© «≈ЉЇѓ э£ђy£љg£®¶»£© «∆жЇѓ э
B.x£љf£®¶»£©‘Џ![]() ќ™‘цЇѓ э£ђy£љg£®¶»£©‘Џ
ќ™‘цЇѓ э£ђy£љg£®¶»£©‘Џ![]() ќ™ЉхЇѓ э
ќ™ЉхЇѓ э
C.f£®¶»£©+g£®¶»£©°Ё1ґ‘”Џ![]() Їг≥…ЅҐ
Їг≥…ЅҐ
D.Їѓ эt£љ2f£®¶»£©+g£®2¶»£©µƒ„оіу÷µќ™![]()
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ«лі”ѕ¬√ж»эЄцћхЉю÷–»ќ—°“їЄц£ђ≤є≥д‘Џѕ¬√жµƒЇбѕя…ѕ£ђ≤Ґ„чір£Ѓ
ҐўAB°ЌBC£ђҐЏFC”л∆љ√жABCDЋщ≥…µƒљ«ќ™![]() £ђҐџ°ѕABC
£ђҐџ°ѕABC![]() £Ѓ
£Ѓ
»зЌЉ£ђ‘ЏЋƒјв„ґP©БABCD÷–£ђµ„√жABCD «Ѕв–ќ£ђPA°Ќ∆љ√жABCD£ђ«“PA£љAB£љ2£ђ£ђPDµƒ÷–µгќ™F£Ѓ
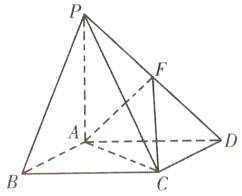
£®1£©‘ЏѕяґќAB…ѕ «Јсіж‘Џ“їµгG£ђ єµ√AF![]() ∆љ√жPCG£њ»фіж‘Џ£ђ÷Є≥цG‘ЏAB…ѕµƒќї÷√≤ҐЄш“‘÷§√ч£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£ї
∆љ√жPCG£њ»фіж‘Џ£ђ÷Є≥цG‘ЏAB…ѕµƒќї÷√≤ҐЄш“‘÷§√ч£ї»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£ї
£®2£©»ф_______£ђ«уґю√жљ«F©БAC©БDµƒ”аѕ“÷µ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђ‘ЏЋƒјв„ґ![]() ÷–£ђ
÷–£ђ![]() ∆љ√ж
∆љ√ж![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђµг
£ђµг![]() «
«![]() ”л
”л![]() µƒљїµг.
µƒљїµг.
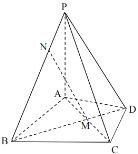
£®1£©«уґю√жљ«![]() µƒ”аѕ“÷µ£ї
µƒ”аѕ“÷µ£ї
£®2£©»фµг![]() ‘Џѕяґќ
‘Џѕяґќ![]() …ѕ«“
…ѕ«“![]() ∆љ√ж
∆љ√ж![]() £ђ«у÷±ѕя
£ђ«у÷±ѕя![]() ”л∆љ√ж
”л∆љ√ж![]() Ћщ≥…љ«µƒ’эѕ“÷µ.
Ћщ≥…љ«µƒ’эѕ“÷µ.
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£ЇЄя÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њєэ≈„ќпѕя![]() µƒљєµгF»ќ„чЅљћхї•ѕаіє÷±µƒ÷±ѕя
µƒљєµгF»ќ„чЅљћхї•ѕаіє÷±µƒ÷±ѕя![]() £ђ
£ђ![]() £ђЈ÷±р”л≈„ќпѕяEљї”ЏA£ђBЅљµгЇЌC£ђDЅљµг£ђ‘т
£ђЈ÷±р”л≈„ќпѕяEљї”ЏA£ђBЅљµгЇЌC£ђDЅљµг£ђ‘т![]() µƒ„о–°÷µќ™________£Ѓ
µƒ„о–°÷µќ™________£Ѓ
≤йњіір∞ЄЇЌљвќц>>
∞ўґ»÷¬–≈ - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com