
【题目】定义在R上的函数f(x)= ![]() x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
x3+cx+3(c为常数),f(x)在x=0处的切线与直线y=x+2垂直.
(1)求函数y=f(x)的解析式;
(2)设g(x)=4lnx﹣f′(x),(其中f′(x)是函数f(x)的导函数),求g(x)的极值.
【答案】
(1)解:f(x)= ![]() x3+cx+3,f′(x)=x2+c,
x3+cx+3,f′(x)=x2+c,
因为f(x)在x=0处的切线与直线y=x+2垂直,
所以f′(0)=c=﹣1,
即f(x)= ![]() x3﹣x+3
x3﹣x+3
(2)解:由(1),可得g(x)=4lnx﹣x2+1,x∈(0,+∞),
则g′(x)= ![]() ﹣2x=
﹣2x= ![]() =﹣
=﹣ ![]() ,
,
①当0<x< ![]() 时,g′(x)>0,
时,g′(x)>0,
可得g(x)在(0, ![]() )上为增函数;
)上为增函数;
②当x≥ ![]() 时,g′(x)≤0,
时,g′(x)≤0,
可得g(x)在( ![]() ,+∞)上为减函数;
,+∞)上为减函数;
所以g(x)在x= ![]() 处取得极大值g(
处取得极大值g( ![]() )=2ln2﹣1
)=2ln2﹣1
【解析】(1)求出f′(x)=x2+c;然后根据f(x)在x=0处的切线与直线y=x+2垂直,求出f′(0)=c=﹣1,进而求出函数y=f(x)的解析式即可;(2)分别求出g(x)、g′(x),然后分两种情况:①当0<x< ![]() 和②当x≥
和②当x≥ ![]() 时,讨论求出g(x)的极值即可.
时,讨论求出g(x)的极值即可.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100]后得到如图的频率分布直方图. 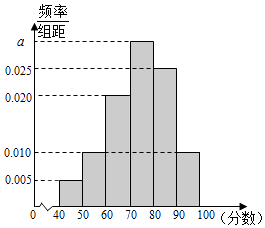
(1)求图中实数a的值;
(2)若该校高二年级共有学生640人,试估计该校高二年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两曲线f(x)= ![]() x2+ax与g(x)=2a2lnx+b有公共点,且在该点处有相同的切线,则a∈(0,+∞)时,实数b的最大值是( )
x2+ax与g(x)=2a2lnx+b有公共点,且在该点处有相同的切线,则a∈(0,+∞)时,实数b的最大值是( )
A.e ![]()
B.2e ![]()
C.e ![]()
D.![]() e
e ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=5sin3x+5 ![]() cos3x,下列说法正确的是( )
cos3x,下列说法正确的是( )
A.函数f(x)关于x= ![]() π对称
π对称
B.函数f(x)向左平移 ![]() 个单位后是奇函数
个单位后是奇函数
C.函数f(x)关于点( ![]() ,0)中心对称
,0)中心对称
D.函数f(x)在区间[0, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内两点A(8,-6),B(2,2).
(1)求过点P(2,-3)且与直线AB平行的直线l的方程;
(2)一束光线从B点射向(1)中直线l,若反射光线过点A,求反射光线所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某体育场要建造一个长方形游泳池,其容积为4800m3 , 深为3m,如果建造池壁的单价为a且建造池底的单价是建造池壁的1.5倍,怎样设计水池的长和宽,才能使总造价最底?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+3x,其中a>0. (Ⅰ)当a=1时,求不等式f(x)≥3x+2的解集
(Ⅱ)若不等式f(x)≤0的解集为{x|x≤﹣1},求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com