
【题目】如图,已知四边形ABCD是边长为2的菱形,∠ABC=60°,平面AEFC⊥平面ABCD,EF∥AC,AE=AB,AC=2EF.
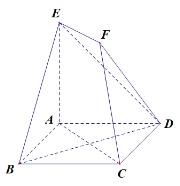
(1)求证:平面BED⊥平面AEFC;
(2)若四边形AEFC为直角梯形,且EA⊥AC,求二面角B-FC-D的余弦值.
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知函数![]() 是奇函数,
是奇函数,![]() 的定义域为
的定义域为![]() .当
.当![]() 时,
时,![]()
![]() .(e为自然对数的底数).
.(e为自然对数的底数).
(1)若函数![]() 在区间
在区间![]() 上存在极值点,求实数
上存在极值点,求实数![]() 的取值范围;
的取值范围;
(2)如果当x≥1时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业引进现代化管理体制,生产效益明显提高.2018年全年总收入与2017年全年总收入相比增长了一倍,实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化.下图给出了该企业这两年不同运营成本占全年总收入的比例,下列说法正确的是( )
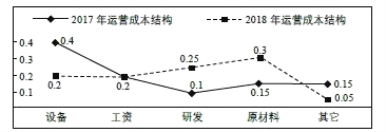
A.该企业2018年原材料费用是2017年工资金额与研发费用的和
B.该企业2018年研发费用是2017年工资金额、原材料费用、其它费用三项的和
C.该企业2018年其它费用是2017年工资金额的![]()
D.该企业2018年设备费用是2017年原材料的费用的两倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A,B关于坐标原点O对称,![]() ,以M为圆心的圆过A,B两点,且与直线
,以M为圆心的圆过A,B两点,且与直线![]() 相切,若存在定点P,使得当A运动时,
相切,若存在定点P,使得当A运动时,![]() 为定值,则点P的坐标为( )
为定值,则点P的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节假期,旅游过年持续火爆.特别是:东北雪乡、梦回大唐、江南水乡、三亚之行这四条路线受到广大人民的热播.现有2个家庭准备去这四个地方旅游,假设每个家庭均从这四条路线中任意选取一条路线去旅源,则两个家庭选择同一路线的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .三角形
.三角形![]() 的两条边
的两条边![]() ,
,![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
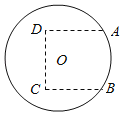
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com