
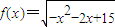 ,集合A={x|y=f(x)},B={y|y=f(x)},则右图中阴影部分表示的集合为( )
,集合A={x|y=f(x)},B={y|y=f(x)},则右图中阴影部分表示的集合为( )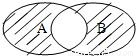
 的定义域和值域,求出集合A与B后,分析韦恩图表示的含义,即可得到结果.
的定义域和值域,求出集合A与B后,分析韦恩图表示的含义,即可得到结果. ,
,

科目:高中数学 来源:2012-2013学年浙江省温州中学高一(上)期中数学试卷(解析版) 题型:选择题
 ,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )
,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州中学高一(上)期中数学试卷(解析版) 题型:选择题
 ,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )
,集合M={x|f(x)=0}={x1,x2,…,x7}⊆N*,设c1≥c2≥c3≥c4,则c1-c4=( )查看答案和解析>>
科目:高中数学 来源:2007-2008学年广东省华南师大附中高三综合测试数学试卷3(文科)(解析版) 题型:选择题
 ,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( )
,集合M={x|f(x)<0},P={x|f'(x)>0},若M?P,则实数a的取值范围是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com