
����Ŀ������ˮΧ�������㼼��������ֳ�ܶȸߡ�����Ч��õ��ص㣮�о�����������ˮΧ��������ʱ��ij������һ���������£�ÿβ���ƽ�������ٶ�v����λ��ǧ��/�꣩����ֳ�ܶ�x ����λ��β/�����ף��ĺ�������x������4β/������ʱ��v��ֵΪ2ǧ��/�ꣻ��4��x��20ʱ��v��x��һ�κ�������x�ﵽ20β/������ʱ����ȱ����ԭ��v��ֵΪ0ǧ��/�꣮
��1����0��x��20ʱ����v����x�ĺ�������ʽ��
��2������ֳ�ܶ�xΪ���ʱ�����������������λ��ǧ��/�����ף����Դﵽ���������ֵ��
���𰸡�
��1���⣺������õ�0��x��4ʱ��v=2��
��4��x��20ʱ����v=ax+b��
����֪�ã� ![]() ����ã�
����ã� 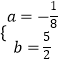 ��
��
����v=�� ![]() x+
x+ ![]() ��
��
�ʺ���v= 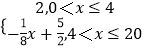
��2���⣺����������Ϊf��x��ǧ��/�����ף�
�����Ⲣ�ɣ�1���ɵ�f��x��= 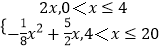
��0��x��4ʱ��f��x��Ϊ����������f��x��max=f��4��=4��2=8��
��4��x��20ʱ��f��x��=�� ![]() x2+
x2+ ![]() x=��
x=�� ![]() ��x2��20x��=��
��x2��20x��=�� ![]() ��x��10��2+
��x��10��2+ ![]() ��
��
f��x��max=f��10��=12.5��
���Ե�0��x��20ʱ��f��x�������ֵΪ12.5��
������ֳ�ܶ�Ϊ10β/������ʱ����������������Դﵽ������ֵΪ12.5ǧ��/������
����������1����4��x��20ʱ����v=ax+b�����ݴ���ϵ�������a��b��ֵ���Ӷ���������Ľ���ʽ���ɣ���2������f��x���ı���ʽ����϶��κ������������f��x�������ֵ���ɣ�


 Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���Sn��4n������{bn}����b1����3��
bn��1��bn��(2n��3)(n��N*)��
(1)������{an}��ͨ�ʽ��
(2)������{bn}��ͨ�ʽ��
(3)��cn��![]() ��������{cn}��ǰn���Tn.
��������{cn}��ǰn���Tn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪y=f��x���Ƕ�����R�ϵ�ż��������x��0ʱ��f��x��=x2��2x��
��1����f��x���Ľ���ʽ��
��2����������f��x����ͼ��ָ���䵥�����䣮������Ҫ�ϸ�֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=e1+|x|�� ![]() ����ʹ��f��x����f��2x��1��������x��ȡֵ��Χ�ǣ� ��
����ʹ��f��x����f��2x��1��������x��ȡֵ��Χ�ǣ� ��
A.![]()
B.![]()
C.���� ![]() ��
�� ![]() ��
��
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ȫ��U=R������A={x|4��2x��128}��B={x|1��x��6}��M={x|a��3��x��a+3}��
��1����A��UB��
��2����M��UB=R����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() .
.

��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��
��![]() �У���֪
�У���֪![]() ����
����![]() ��
�� ![]() ��������
��������![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�
������![]() ������
������![]() ��ͨ�ʽ��
��ͨ�ʽ��
������![]() ���Ƿ����������
���Ƿ����������![]() ��
�� ![]() ��
��![]() ����ʹ
����ʹ![]() ��
�� ![]() ��
�� ![]() �ɵȲ����У������ڣ����
�ɵȲ����У������ڣ����![]() ��
�� ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��֪ƽ��ֱ������ϵ![]() ����
����![]() Ϊ���㣬
Ϊ���㣬 ![]() ��ķǸ�����Ϊ���Ὠ��������ϵ��
��ķǸ�����Ϊ���Ὠ��������ϵ�� ![]() ��ļ�����Ϊ
��ļ�����Ϊ![]() ������
������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������.
������.
��1��д����![]() ��ֱ�����꼰����
��ֱ�����꼰����![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2����![]() ����
Ϊ����![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ���е�
���е�![]() ��ֱ��
��ֱ��![]() ��
�� ![]() �ľ������Сֵ.
�ľ������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ݺ���y= ![]() ��m��Z����ͼ����x�ᣬy��û�н��㣬�ҹ���y��Գƣ���m=�� ��
��m��Z����ͼ����x�ᣬy��û�н��㣬�ҹ���y��Գƣ���m=�� ��
A.1
B.0��2
C.��1��1��3
D.0��1��2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com