
【题目】自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程。

【答案】已知圆的标准方程是(x-2)2+(y-2)2=1,它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1。设光线L所在的直线的方程是y-3=k(x+3)(其中斜率k待定),由题设知对称圆的圆心C′(2,-2)到这条直线的距离等于1,即d=![]() =1。整理得 12k2+25k+12=0,解得k= -
=1。整理得 12k2+25k+12=0,解得k= -![]() 或k= -
或k= -![]() 。故所求直线方程是y-3= -
。故所求直线方程是y-3= -![]() (x+3),或y-3= -
(x+3),或y-3= -![]() (x+3),即3x+4y-3=0或4x+3y+3=0。
(x+3),即3x+4y-3=0或4x+3y+3=0。
【解析】试题分析:已知圆![]() 关于
关于![]() 轴的对称圆
轴的对称圆![]() 的方程为
的方程为
![]() 2分
2分
如图所示.
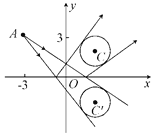
可设光线![]() 所在直线方程为
所在直线方程为![]() , 4分
, 4分
∵直线![]() 与圆
与圆![]() 相切,
相切,
∴圆心![]()
![]() 到直线
到直线![]() 的距离
的距离![]() =
=![]() , 6分
, 6分
解得![]() 或
或![]() . 10分
. 10分
∴光线![]() 所在直线的方程为
所在直线的方程为![]() 或
或![]() .…12分
.…12分


科目:高中数学 来源: 题型:
【题目】以边长为4的等比三角形![]() 的顶点
的顶点![]() 以及
以及![]() 边的中点
边的中点![]() 为左、右焦点的椭圆过
为左、右焦点的椭圆过![]() 两点.
两点.
(1)求该椭圆的标准方程;
(2)过点![]() 且
且![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() 两点,求证直线
两点,求证直线![]() 与
与![]() 的交点在一条直线上.
的交点在一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
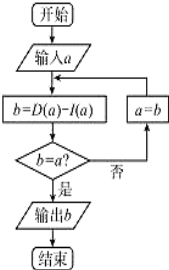
A.792 B.693
C.594 D.495
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为![]() ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为![]() ,而当年产销量相等。
,而当年产销量相等。
(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中a>0.
万元,其中a>0.
(1)若设备升级后生产这批A产品的利润不低于原来生产该批A产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批B产品的利润始终不高于设备升级后生产这批A产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com