
【题目】已知![]() ,函数
,函数![]() .
.
(1)若![]() ,证明:函数
,证明:函数![]() 在区间
在区间![]() 上是单调增函数;
上是单调增函数;
(2)求函数![]() 在区间
在区间![]() 上的最大值;
上的最大值;
(3)若函数![]() 的图像过原点,且
的图像过原点,且![]() 的导数
的导数![]() ,当
,当![]() 时,函数
时,函数![]() 过点
过点![]() 的切线至少有2条,求实数
的切线至少有2条,求实数![]() 的值.
的值.
【答案】(1)证明见解析;(2)当![]() 时,最大值为
时,最大值为![]() ;当
;当![]() 时,最大值为
时,最大值为![]() (3)
(3)![]()
【解析】
(1)由题![]() ,利用导函数求单调区间即可;
,利用导函数求单调区间即可;
(2)利用导数可以推导得到![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数,则当
上是增函数,则当![]() 时,
时,![]() 的最大值为
的最大值为![]() 和
和![]() 中的最大值,作差可得
中的最大值,作差可得![]() ,设
,设![]() ,再次利用导数推导
,再次利用导数推导![]() 的单调性,进而得到
的单调性,进而得到![]() 上的最大值;
上的最大值;
(3)由题可得![]() ,设切点为
,设切点为![]() ,则
,则![]() 处的切线方程为:
处的切线方程为:![]() ,将
,将![]() 代入可得
代入可得![]() ,则将原命题等价为关于
,则将原命题等价为关于![]() 的方程至少有2个不同的解,设
的方程至少有2个不同的解,设![]() ,进而利用导函数判断
,进而利用导函数判断![]() 的单调性,从而求解即可
的单调性,从而求解即可
(1)证明:![]() ,则
,则![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]()
![]() ,即此时函数
,即此时函数![]() 在区间
在区间![]() 上是单调增函数.
上是单调增函数.
(2)由(1)知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调增函数,
上是单调增函数,
当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,则
,则![]() 在区间
在区间![]() 上是单调减函数;
上是单调减函数;
同理,当![]() 时,
时,![]() 在区间
在区间![]() 上是单调增函数,在区间
上是单调增函数,在区间![]() 上是单调减函数;
上是单调减函数;
即当![]() ,且
,且![]() 时,
时,![]() 在区间
在区间![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数,
上是增函数,
则当![]() 时,
时,![]() 的最大值为
的最大值为![]() 和
和![]() 中的最大值,
中的最大值,
![]() ,
,
![]() 令
令![]() ,
,
则 ,
,
![]()
![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,此时最大值为
,此时最大值为![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,此时最大值为
,此时最大值为![]() .
.
(3)![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 的图像过原点,
的图像过原点,
![]() ,即
,即![]() ,则
,则![]() ,
,
设切点为![]() ,则
,则![]() 处的切线方程为:
处的切线方程为:![]() ,
,
将![]() 代入得
代入得![]() ,
,
即![]() (※),
(※),
则原命题等价为关于![]() 的方程(※)至少有2个不同的解,
的方程(※)至少有2个不同的解,
设![]() ,
,
则![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
当![]() 和
和![]() 时,
时,![]() ,此时函数
,此时函数![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 减函数,
减函数,
![]()
![]() 的极大值为
的极大值为![]() ,
,
![]() 的极小值为
的极小值为![]() ,
,
设![]() ,则
,则![]() ,则原命题等价为
,则原命题等价为![]() ,即
,即![]() 对
对![]() 恒成立,
恒成立,
![]() 由
由![]() 得
得![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() 的最大值为
的最大值为![]() ,
,![]()
![]() ,
,
故![]() ,
,
综上所述,当![]() 时,函数
时,函数![]() 过点
过点![]() 的切线至少有2条,此时实数m的值为
的切线至少有2条,此时实数m的值为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:

经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;②
;②![]() ;③
;③![]() ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备
,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(ⅰ)若从设备![]() 的生产流水线上随意抽取
的生产流水线上随意抽取![]() 件零件,求恰有一件次品的概率;
件零件,求恰有一件次品的概率;
(ⅱ)若从样本中随意抽取![]() 件零件,计算其中次品个数
件零件,计算其中次品个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
(1)若用分层抽样的方法从“优秀警员”和“优秀陪练员”中共提取10人,然后再从这10人中选4人,那么至少有1人是“优秀警员”的概率是多少?
(2)若所有“优秀警员”中选3名代表,用![]() 表示所选女“优秀警员”的人数,试求
表示所选女“优秀警员”的人数,试求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
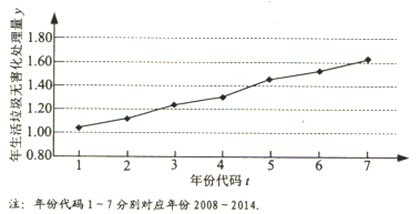
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某冰糖橙,甜橙的一种,云南著名特产,以味甜皮薄著称。该橙按照等级可分为四类:珍品、特级、优级和一级(每箱有5kg),某采购商打算订购一批橙子销往省外,并从采购的这批橙子中随机抽取100箱,利用橙子的等级分类标准得到的数据如下表:
等级 | 珍品 | 特级 | 优级 | 一级 |
箱数 | 40 | 30 | 10 | 20 |
(1)若将频率改为概率,从这100箱橙子中有放回地随机抽取4箱,求恰好抽到2箱是一级品的概率:
(2)利用样本估计总体,庄园老板提出两种购销方案供采购商参考:
方案一:不分等级卖出,价格为27元/kg;
方案二:分等级卖出,分等级的橙子价格如下:
等级 | 珍品 | 特级 | 优级 | 一级 |
售价(元/kg) | 36 | 30 | 24 | 18 |
从采购商的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的是珍品等级,求x的分布列及数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考数学考试中有12道选择题,每道选择题有4个选项,其中有且仅有一个是正确的.评分标准规定:在每小题给出的四个选项中,只有一项是符合题目要求的,答对得5分,不答或答错得0分.某考生每道选择题都选出一个答案,能确定其中有8道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的,有一道题能判断出一个选项是错误的,还有一道题因不理解题意只能乱猜.试求该考生的选择题:
(1)得60分的概率;
(2)得多少分的概率最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com