
【题目】若函数 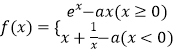 没有零点,则实数a的取值范围是 .
没有零点,则实数a的取值范围是 .
【答案】(﹣2,e)
【解析】解:当x<0时, ![]() ,
,
当x∈(﹣∞,﹣1)时,f'(x)>0,f(x)单调递增,
当x∈(﹣1,0)时,f'(x)<0,f(x)单调递减,
所以当x=﹣1时,f(x)取得极大值f(﹣1)=﹣2﹣a,根据题意,﹣2﹣a<0,a>﹣2;
当x≥0时,f'(x)=ex﹣a,当a∈(﹣2,1]时,f'(x)≥0,f(x)单调递增,
所以fmin(x)=f(0)=1>0,满足题意;
当a>1时,令f'(x)=0,得x=lna,
当x∈[0,lna)时,f'(x)<0,f(x)单调递减,
当x∈(lna,+∞)时,f'(x)>0,f(x)单调递增,
所以当x=lna时,f(x)取得极大值f(lna)=a﹣alna,根据题意,a﹣alna>0,
所以1﹣lna>0,lna<1,a<e,
∴a∈(1,e),
综上所述,实数a的取值范围是(﹣2,e).
故答案为:(﹣2,e).
在分段函数上根据不同的解析式进行讨论,求导根据单调性,得出极值,可得a的取值范围.


科目:高中数学 来源: 题型:
【题目】已知命题p:“存在x0∈[1,+∞),使得(log23) ![]() ≥1”,则下列说法正确的是( )
≥1”,则下列说法正确的是( )
A.p是假命题;¬p“任意x∈[1,+∞),都有(log23)x<1”
B.p是真命题;¬p“不存在x0∈[1,+∞),使得(log23) ![]() <1”
<1”
C.p是真命题;¬p“任意x∈[1,+∞),都有(log23)x<1”
D.p是假命题;¬p“任意x∈(﹣∞,1),都有(log23)x<1”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中.以原点为极点,x轴的正半轴为极轴建立极坐标系已知曲线C:pcos2θ=2asinθ(a>0)过点P(﹣4,﹣2)的直线l的参数方程为 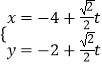 (t为参数)直线l与曲线C分别交于点M,N.
(t为参数)直线l与曲线C分别交于点M,N.
(1)写出C的直角坐标方程和l的普通方程;
(2)若丨PM丨,丨MN丨,丨PN丨成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知ABCD为平行四边形,∠A=60°,线段AB上点F满足AF=2FB,AB长为12,点E在CD上,EF∥BC,BD⊥AD,BD与EF相交于N.现将四边形ADEF沿EF折起,使点D在平面BCEF上的射影恰在直线BC上.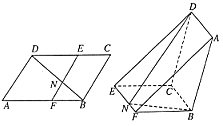
(Ⅰ)求证:BD⊥平面BCEF;
(Ⅱ)求折后直线DE与平面BCEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,M是AD上一点.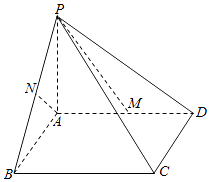
(1)求证:AB⊥PM;
(2)若N是PB的中点,且AN∥平面PCM,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴,两坐标系中的单位长度相同,已知曲线C的极坐标方程为ρ=2(sinθ+cosθ).
(Ⅰ)求C的直角坐标方程;
(Ⅱ)直线 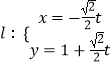 (t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
(t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点为F,右顶点为E,P为直线x=
,右焦点为F,右顶点为E,P为直线x= ![]() a上的任意一点,且(
a上的任意一点,且( ![]() +
+ ![]() )
) ![]() =2.
=2.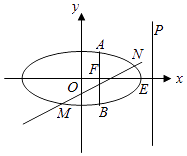
(Ⅰ)求椭圆C的方程;
(Ⅱ)过F垂直于x轴的直线AB与椭圆交于A,B两点(点A在第一象限),动直线l与椭圆C交于M,N两点,且M,N位于直线AB的两侧,若始终保持∠MAB=∠NAB,求证:直线MN的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an﹣1xn﹣1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an﹣1)x+an﹣2)x+…+a1)x+a0 , 首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )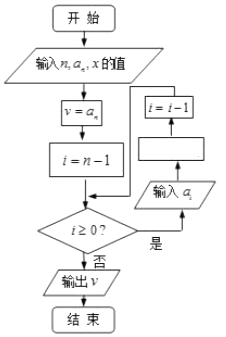
A.v=vx+ai
B.v=v(x+ai)
C.v=aix+v
D.v=ai(x+v)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合U={1,2,…,100},TU.对数列{an}(n∈N*),规定:
①若T=,则ST=0;
②若T={n1 , n2 , …,nk},则ST=a ![]() +a
+a ![]() +…+a
+…+a ![]() .
.
例如:当an=2n,T={1,3,5}时,ST=a1+a3+a5=2+6+10=18.
已知等比数列{an}(n∈N*),a1=1,且当T={2,3}时,ST=12,求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com