【题目】某某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组： 
，并整理得到如下频率分布直方图：
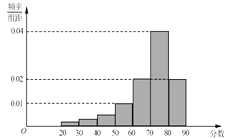
（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40,50）内的人数；
（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．
【答案】(1)0.4.
(2)20人.
(3) 
.
【解析】
分析：(1)根据频率分布直方图可知,即可求解样本中分数不小于70的频率，进而得到
分数小于70的概率；
(2)根据题意，根据样本中分数不小于50的频率为
，求得分数在区间
内的人数为5人，进而求得总体中分数在区间内的人数；
（3）由题意可知，样本中分数不小于70的学生人数为60人，求得样本中分数不小于70的男生人数，即可求解.
详解：(1)根据频率分布直方图可知,样本中分数不小于70的频率为
(0.02+0.04)×10=0.6 ,
样本中分数小于70的频率为1-0.6=0.4.
∴从总体的400名学生中随机抽取一人其分数小于70的概率估计为0.4
(2)根据题意，样本中分数不小于50的频率为
，
分数在区间
内的人数为
．
所以总体中分数在区间内的人数估计为
．
（3）由题意可知，样本中分数不小于70的学生人数为
，
所以样本中分数不小于70的男生人数为
所以样本中的男生人数为
，女生人数为
，男生和女生人数的比例为
挑战100单元检测试卷系列答案科目：高中数学 来源： 题型：
【题目】（本小题满分12分）已知圆C过点P（1，1），且与圆M：
关于直线
对称．
（1）求圆C的方程：
（2）设Q为圆C上的一个动点，求
最小值；
（3）过点P作两条相异直线分别与圆C交与A，B，且直线ＰＡ和直线ＰＢ的倾斜角互补，Ｏ为坐标原点，试判断直线ＯＰ与直线ＡＢ是否平行？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
的底面是菱形，
底面
，
分别是
的中点，
，
，
.
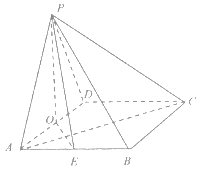
（I）证明：
；
（II）求直线
与平面
所成角的正弦值；
（III）在
边上是否存在点
，使
与
所成角的余弦值为
，若存在，确定点位置；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
．
（1）当
时，求曲线
在
处的切线方程；
（2）当
时，求函数的单调区间；
（3）在（2）的条件下，设函数
，若对于
，
，使
成立，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某家庭记录了未使用节水龙头50天的日用水量数据（单位：
）和使用了节水龙头50天的日用水量数据，得到频数分布表如下：
未使用节水龙头50天的日用水量频数分布表
日用水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) | [0.6,0.7) |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
（1）作出使用了节水龙头50天的日用水量数据的频率分布直方图；
（2）估计该家庭使用节水龙头后，日用水量小于0.3的概率；
（3）估计该家庭用节水龙头后，一年能节省多少水.（一年按365天计算，同一组中的数据以这组数据所在区间中点的值作代表）
查看答案和解析>>
科目：高中数学 来源： 题型：
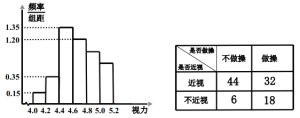
【题目】眼保健操是一种眼睛的保健体操，主要是通过按摩眼部穴位，调整眼及头部的血液循环，调节肌肉，改善眼的疲劳，达到预防近视等眼部疾病的目的.某学校为了调查推广眼保健操对改善学生视力的效果，在应届高三的全体800名学生中随机抽取了100名学生进行视力检查，并得到如图的频率分布直方图.
（1）若直方图中后三组的频数成等差数列，试估计全年级视力在5.0以上的人数；
（2）为了研究学生的视力与眼保健操是否有关系，对年级不做眼保健操和坚持做眼保健操的学生进行了调查，得到下表中数据，根据表中的数据，能否在犯错的概率不超过0.005的前提下认为视力与眼保健操有关系？
（3）在（2）中调查的100名学生中，按照分层抽样在不近视的学生中抽取8人，进一步调查他们良好的护眼习惯，在这8人中任取2人，记坚持做眼保健操的学生人数为X，求X的分布列和数学期望.
附：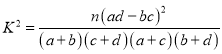
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随机抽取某厂的某种产品400件，经质检，其中有一等品252件、二等品100件、三等品40件、次品8件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元.设1件产品的利润（单位：万元）为
.
（1）求的分布列和1件产品的平均利润（即的期望）；
（2）经技术革新后，仍有四个等级的产品，但次品率降为1%，一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.75万元，则三等品率最多是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某娱乐节目参赛选手分初赛培训、复赛三个阶段选拔，将50位参选手的初赛成绩（总分150分）分成[90，100），[100，110），[110，120），[120，130），[130，140）5组进行统计，得到如图所示的频率分布直方图.
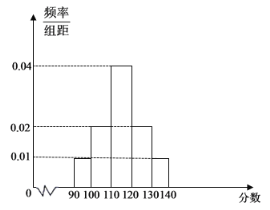
（1）根据频率分析直方图，估算这50个选手初赛成绩的平均分，若节日组规定成绩大于或等于120分的选手可获得节目组组织的培训资格，120分以下（不包括120）的则被淘汰，求这50个人中获得培训资格的人数；
（2）节目组从获得培训资格的人员中选拔部分人员进入复赛.为增加节目的娱乐性，节目组提供了以下两种进入复赛的方式（每位选手只能选择其中一种）
第一种方式：利用分层抽样的方法抽取6名选手参加复赛；
第二种方式：每人最多有5次答题机会，累计答对3题或答错3题终止答题，答对3题可参加复赛
①已知甲的初赛成绩在[120，130）内，他答对每一个问题的概率为
，并且互相之间没有影响甲要想参加复赛，选择那种方式更有利？
②若甲选择第二种方式，求他在答题过程中答题个数X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
