【题目】若函数y=f（x）图象上存在不同的两点A，B关于y轴对称，则称点对[A，B]是函数y=f（x）的一对“黄金点对”（注：点对[A，B]与[B，A]可看作同一对“黄金点对”）．已知函数f（x）=
，则此函数的“黄金点对“有（ ）
A. 0对B. 1对C. 2对D. 3对
科目：高中数学 来源： 题型：
【题目】某企业招聘大学毕业生，经过综合测试，录用了14名女生和6名男生，这20名学生的测试成绩如茎叶图所示(单位：分)，记成绩不小于80分者为
等，小于80分者为
等．
(1)求女生成绩的中位数及男生成绩的平均数；
(2)如果用分层抽样的方法从等和等中共抽取5人组成“创新团队”，则从等和等中分别抽几人？
(3)在(2)问的基础上，现从该“创新团队”中随机抽取2人，求至少有1人是等的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（n）=1+ 
+ 
+…+ 
（n∈N*），计算得f（2）= 
，f（4）＞2，f（8）＞ 
，f（16）＞3，f（32）＞ 
，由此推算：当n≥2时，有（ ）
A.f（2n）＞ 
（n∈N*）
B.f（2n）＞ 
（n∈N*）
C.f（2n）＞ （n∈N*）
D.f（2n）＞ 
（n∈N*）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，圆C的方程为（x+6）2+y2=25． （Ⅰ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；
（Ⅱ）直线l的参数方程是 
（t为参数），l与C交与A，B两点，|AB|= 
，求l的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)
男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:
，
，
，
，
，
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ax2-4ax+1+b（a＞0）的定义域为[2，3]，值域为[1，4]；设g（x）=
．
（1）求a，b的值；
（2）若不等式g（2x）-k2x≥0在x∈[1，2]上恒成立，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为改善职工的出行条件，随机抽取50名职工，调查他们的居住地与公司的距离d（单位：千米）．若样本数据分组为[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]，由数据绘制的分布频率直方图如图所示，则样本中职工居住地与公司的距离不超过4千米的人数为人．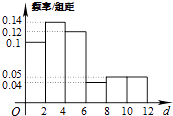 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：“方程x2﹣ax+a+3=0有解”，q：“ 
﹣a≥0在[0，+∞）上恒成立”，若p或q为真命题，p且q为假命题，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
