若函数f（x）=ex-2x-a在R上有两个零点，则实数a的取值范围是 ．
【答案】
分析：画出函数f（x）=e
x-2x-a的简图，欲使函数f（x）=e
x-2x-a在R上有两个零点，由图可知，其极小值要小于0．由此求得实数a的取值范围．
解答：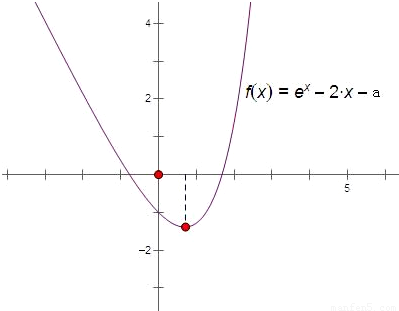
解：令f，（x）=e
x-2=0，则x=ln2，
∴x＞ln2，f，（x）=e
x-2＞0；
x＜ln2，f，（x）=e
x-2＜0；
∴函数f（x）在（ln2，+∞）上是增函数，在（-∞，ln2）上是减函数．
∵函数f（x）=e
x-2x-a在R上有两个零点，
所以f（ln2）=2-2ln2-a＜0，
故a＞2-2ln2．
故填：（2-2ln2，+∞）．
点评：本题主要考查函数的零点以及数形结合方法，数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质；另外，由于使用了数形结合的方法，很多问题便迎刃而解，且解法简捷．
