
【题目】如图,![]() 是等边三角形,
是等边三角形, ![]() 是
是![]() 边上的动点(含端点),记
边上的动点(含端点),记![]() ,
,![]() .
.
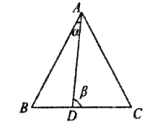
(1)求![]() 的最大值;
的最大值;
(2)若![]() ,求
,求![]() 的面积.
的面积.
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】已知A、B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径,则![]() 的取值范围是( )
的取值范围是( )
A. [![]() ,0) B. [
,0) B. [![]() ,0] C. [
,0] C. [![]() ,1) D. [
,1) D. [![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD—A1B1C1D1中,AB=BD=1,![]() ,AA1=BC=2,AD∥BC.
,AA1=BC=2,AD∥BC.

(1)证明:BD⊥平面ABB1A1.
(2)比较四棱锥D—ABB1A1与四棱锥D—A1B1C1D1的体积的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下面平面几何中的常见结论在立体几何中也成立的所有序号______.
①四边形内角和为![]() ;
;
②垂直的两条直线必相交;
③垂直同一条直线的两条直线平行;
④平行同一条直线的两条直线平行;
⑤四边相等的四边形,其对角线垂直;
⑥到三角形三边距离相等的点是这个三角形的内心;
⑦到一个角的两边距离相等的点必在这个角的角平分线上;
⑧在平面几何中有“一组平行线(至少3条)被两条直线所截得的对应线段成比例”的结论,则这一结论可推广到立体几何中“一组平行平面(至少3个)被两条直线所截得的对应线段也成比例.”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂经过节能降耗技术改进后生产甲产品x吨与相应的生产耗能y吨间的几组数据
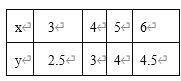
(1)试画出此表中数据对应的散点图 ;
(2)若变量y与x线性相关 ,试求出线性回归方程y = b x + a ;
(3)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤 ,试根据(2)求出的线性回归方程 ,预测生产100吨甲产品的生产耗能比技改前降低多少吨标准煤?
(参考公式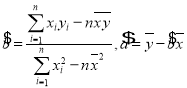 ,)
,)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为![]() (t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)求曲线C1的极坐标方程和C2的直角坐标方程;
(2)射线OP:![]() (其中
(其中![]() )与C2交于P点,射线OQ:
)与C2交于P点,射线OQ:![]() 与C2交于Q点,求
与C2交于Q点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构对某校高二文科学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)试根据(2)中求出的线性回归方程,预测记忆力为14的学生的判断力.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com