
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的解析式;
的解析式;
(2)求![]() 的值域,设
的值域,设![]() ,
,![]() 为实数),求
为实数),求![]() 在
在![]() 时的最大值
时的最大值![]() ;
;
(3)对(2)中![]() ,若
,若![]() 对
对![]() 的所有实数
的所有实数![]() 及
及![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;
(2)![]() ,
,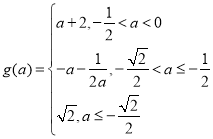 ;
;
(3)![]() 或
或![]() .
.
【解析】
(1)由![]() 且
且![]() 可求得定义域,可得
可求得定义域,可得![]() 的解析式;
的解析式;
(2)![]() ,令
,令![]() ,则
,则![]() ,由此可转化为关于
,由此可转化为关于![]() 的二次函数,按照对称轴
的二次函数,按照对称轴![]() 与
与![]() 的范围
的范围![]() ,
,![]() 的位置关系分三种情况讨论,借助单调性即可求得其最大值;
的位置关系分三种情况讨论,借助单调性即可求得其最大值;
(3)先由(2)求出函数![]() 的最小值,
的最小值,![]() 对
对![]() 恒成立,即要使
恒成立,即要使![]() 恒成立,从而转化为关于
恒成立,从而转化为关于![]() 的一次不等式,再根据一次函数的单调性可得不等式组,解出即可.
的一次不等式,再根据一次函数的单调性可得不等式组,解出即可.
(1)由![]() 且
且![]() ,得
,得![]() ,
,
所以函数的定义域为![]() .
.
又![]() ;
;
(2)![]()
![]() ,
,
由![]() ,且
,且![]() ,得
,得![]() .
.
令![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,
由题意知![]() 即为函数
即为函数![]() ,
,![]() 的最大值.
的最大值.
注意到直线![]() 是抛物线
是抛物线![]() 的对称轴,
的对称轴,
因为![]() 时,函数
时,函数![]() ,
,![]() 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
①若![]() ,即
,即![]() ,则
,则![]()
![]() ;
;
②若![]() ,即
,即![]() ,则
,则![]()
![]() ;
;
③若![]() ,即
,即![]() ,则
,则![]()
![]()
![]() ,
,
综上有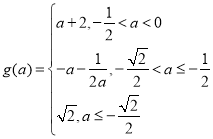 ;
;
(3)由![]() 的解析式可得
的解析式可得![]() 时,
时,![]()
![]() ,
,![]() ;
;
![]() 时,
时,![]()
![]() ;
;
可得![]()
![]() ,
,
由![]() 对
对![]() 恒成立,
恒成立,
即要使![]() 恒成立,
恒成立,
![]() ,令
,令![]() ,
,
对所有的![]() ,
,![]() 成立,
成立,
只需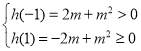 ,即有
,即有 ,
,
解得![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加. 现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(1)设![]() 为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件
为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件![]() 发生的概率
发生的概率
(2)设![]() 为选出的4人中种子选手的人数,求随机变量
为选出的4人中种子选手的人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E的方程为![]() +
+![]() =1(a
=1(a![]() b
b![]() 0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足
0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足![]() =2
=2![]() ,直线OM的斜率为
,直线OM的斜率为![]() 。
。
(1)求E的离心率e。
(2)设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为![]() ,求E的方程
,求E的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A-EFCB中,![]() 为等边三角形,平面AEF
为等边三角形,平面AEF![]() 平面EFCB,
平面EFCB,![]() ,
,![]() ,
,![]() ,
,![]() ,O为EF的中点.
,O为EF的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角F-AE-B的余弦值;
(Ⅲ)若BE![]() 平面AOC,求a的值.
平面AOC,求a的值.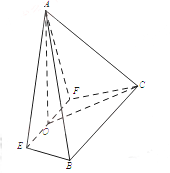
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 的对边分别为
的对边分别为![]() 且
且![]() 为锐角,问:(1)证明: B - A =
为锐角,问:(1)证明: B - A = ![]() ,(2)求 sin A + sin C 的取值范围
,(2)求 sin A + sin C 的取值范围
(1)(1)证明:![]()
(2)(2)求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是双曲线
是双曲线 ![]() 的右焦点,过点
的右焦点,过点 ![]() 作
作 ![]() 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ![]() ,线段
,线段 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,记点
,记点 ![]() 到
到 ![]() 的两条渐近线的距离之积为
的两条渐近线的距离之积为 ![]() ,若
,若 ![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.![]()
B.2
C. 3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位附近只有甲,乙两个临时停车场,它们各有50个车位,为了方便市民停车,某互联网停车公司对这两个停车场在工作日某些固定时刻的剩余停车位进行记录,如下表:
时间 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
停车场甲 | 10 | 3 | 12 | 6 | 12 | 17 |
停车场乙 | 13 | 4 | 3 | 2 | 6 | 19 |
如果表中某一时刻停车场剩余停车位数低于总车位数的10%,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(Ⅰ)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(Ⅱ)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(Ⅲ)当停车场乙发出饱和警报时,求停车场甲也发出饱和警报的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com