
分析 根据函数零点存在定理,可判断①;根据正切函数的单调性,可判断②;根据函数周期性,可判断③;根据定义域不关于原点对称的函数,是非奇非偶函数,可判断④;根据x=-$\frac{1}{3}$时,两个向量反向,可判断⑤.
解答 解:①已知用二分法求方程3x+3x-8=0在x∈(1,2)内的近似解过程中得:
f(1)<0,f(1.5)>0,f(1.25)<0,
则方程的根落在区间(1.25,1.5),故正确;
②y=tanx在它的定义域内,图象不连续,不具有单调性,故错误;
③函数y=$\frac{tanx}{1-tanx}$的最小正周期为π,故正确,
④函数f(x)=$\frac{1+sinx-cosx}{1+sinx+cosx}$的定义域为:{x|x≠π+2kπ,且|x≠-$\frac{π}{2}$+2kπ,k∈Z}不关于原点对称,故函数是非奇非偶函数,故④错误;
⑤已知$\overrightarrow{AB}$=(x,2x),$\overrightarrow{AC}$=(-3x,2),若∠BAC是钝角,则x的取值范围是x<$-\frac{1}{3}$,或$-\frac{1}{3}$<x<0或x>$\frac{4}{3}$,故⑤错误;
故正确的说法是:①③,
故答案为:①③
点评 本题以命题的真假判断与应用为载体,考查了零点存在定理,函数的单调性,函数的周期性,函数的奇偶性,向量的夹角等知识点,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
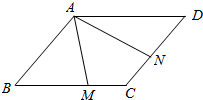 如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.
如图,已知菱形ABCD的边长为2,∠BAD=120°,M,N分别为BC、CD上的点,$\overrightarrow{BM}$=λ$\overrightarrow{BC}$,$\overrightarrow{DN}$=μ$\overrightarrow{DC}$,λ,μ∈(0,1),记$\overrightarrow{AM}$=$\overrightarrow{a}$,$\overrightarrow{AN}$=$\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{7}{4},+∞)$ | B. | [-2,+∞) | C. | (-∞,-2] | D. | $[-2,-\frac{7}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {-1,0} | C. | {-2,3,4} | D. | {2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com