
【题目】以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线的参数方程
轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线的参数方程![]() 为参数
为参数![]() )曲线
)曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
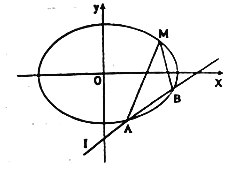
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() :
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两不同的点.
两不同的点.
(1)求椭圆的方程;
(2)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() ,
, ![]() 与
与![]() 轴围成等腰三角形.
轴围成等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 和
和![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: 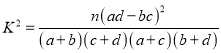 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(3﹣ax)(a>0,a≠1)
(1)当a=3时,求函数f(x)的定义域;
(2)若g(x)=f(x)﹣loga(3+ax),请判定g(x)的奇偶性;
(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+k,且log2f(a)=2,f(log2a)=k,a>0,且a≠1.
(1)求a,k的值;
(2)当x为何值时,f(logax)有最小值?求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2 ![]() . (Ⅰ)判断f(x)奇偶性并证明;
. (Ⅰ)判断f(x)奇偶性并证明;
(Ⅱ)用单调性定义证明函数g(x)= ![]() 在函数f(x)定义域内单调递增,并判断f(x)=log2
在函数f(x)定义域内单调递增,并判断f(x)=log2 ![]() 在定义域内的单调性.
在定义域内的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com