
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的圾坐标方
).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的圾坐标方![]() ,且直线l与曲线C相交于A,B两点.
,且直线l与曲线C相交于A,B两点.
(1)求曲线C的普通方程和l的直角坐标方程;
(2)若![]() ,点
,点![]() 满足
满足![]() ,求此时r的值.
,求此时r的值.
科目:高中数学 来源: 题型:
【题目】2020年全球爆发新冠肺炎,人感染了新冠肺炎病毒后常见的呼吸道症状有:发热、咳嗽、气促和呼吸困难等,严重时会危及生命.随着疫情的发展,自2020年2月5日起,武汉大面积的爆发新冠肺炎,政府为了及时收治轻症感染的群众,逐步建立起了14家方舱医院,其中武汉体育中心方舱医院从2月12日开舱至3月8日闭仓,累计收治轻症患者1056人.据部分统计该方舱医院从2月26日至3月2日轻症患者治愈出仓人数的频数表与散点图如下:
日期 | 2.26 | 2.27 | 2.28 | 2.29 | 3.1 | 3.2 |
序号 | 1 | 2 | 3 | 4 | 5 | 6 |
出仓人数 | 3 | 8 | 17 | 31 | 68 | 168 |

根据散点图和表中数据,某研究人员对出仓人数![]() 与日期序号
与日期序号![]() 进行了拟合分析.从散点图观察可得,研究人员分别用两种函数①
进行了拟合分析.从散点图观察可得,研究人员分别用两种函数①![]() ②
②![]() 分析其拟合效果.其相关指数
分析其拟合效果.其相关指数![]() 可以判断拟合效果,R2越大拟合效果越好.已知
可以判断拟合效果,R2越大拟合效果越好.已知![]() 的相关指数为
的相关指数为![]() .
.
(1)试根据相关指数判断.上述两类函数,哪一类函数的拟合效果更好?(注:相关系数![]() 与相关指数R2满足
与相关指数R2满足![]() ,参考数据表中
,参考数据表中![]() )
)
(2)①根据(1)中结论,求拟合效果更好的函数解析式;(结果保留小数点后三位)
②3月3日实际总出仓人数为216人,按①中的回归模型计算,差距有多少人?
(附:对于一组数据![]() ,其回归直线为
,其回归直线为![]()
相关系数
参考数据:
|
|
|
|
|
|
|
|
|
3.5 | 49.17 | 15.17 | 3.13 | 894.83 | 19666.83 | 10.55 | 13.56 | 3957083 |
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一、二、三、四年级本科生人数之比为6:5:5:4,则应从一年级中抽取90名学生
B.10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率为![]()
C.已知变量x与y正相关,且由观测数据算得![]() =3,
=3,![]() =3.5,则由该观测数据算得的线性回归方程可能是
=3.5,则由该观测数据算得的线性回归方程可能是![]() =0.4x+2.3
=0.4x+2.3
D.从装有2个红球和2个黑球的口袋内任取2个球,至少有一个黑球与至少有一个红球是两个互斥而不对立的事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别是双曲线
的左、右顶点分别是双曲线![]() :
:![]() 的左、右焦点,且
的左、右焦点,且![]() 与
与![]() 相交于点(
相交于点(![]() ).
).
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() 与椭圆
与椭圆![]() 交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地贯彻党的“五育并举”的教育方针,某市要对全市中小学生“体能达标”情况进行了解,决定通过随机抽样选择几个样本校对学生进行体能达标测试,并规定测试成绩低于60分为不合格,否则为合格,若样本校学生不合格人数不超过其总人数的5%,则该样本校体能达标为合格.已知某样本校共有1000名学生,现从中随机抽取40名学生参加体能达标测试,首先将这40名学生随机分为甲、乙两组,其中甲乙两组学生人数的比为3:2,测试后,两组各自的成绩统计如下:甲组的平均成绩为70,方差为16,乙组的平均成绩为80,方差为36.
(1)估计该样本校学生体能测试的平均成绩;
(2)求该样本校40名学生测试成绩的标准差s;
(3)假设该样本校体能达标测试成绩服从正态分布![]() ,用样本平均数
,用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差s作为
,用样本标准差s作为![]() 的估计值
的估计值![]() ,利用估计值估计该样本校学生体能达标测试是否合格?
,利用估计值估计该样本校学生体能达标测试是否合格?
(注:1.本题所有数据的最后结果都精确到整数;2若随机变量z服从正态分布,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设各项均为正数的数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,且
,且![]() ,对一切
,对一切![]() 都成立.
都成立.
(1)当![]() 时,证明数列
时,证明数列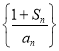 是常数列,并求数列
是常数列,并求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使数列
,使数列![]() 是等差数列?若存在,求出
是等差数列?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为坐标原点,过点
为坐标原点,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() ,
,![]() ,试探究:
,试探究:![]() 是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com