
【题目】正项数列:![]() ,满足:
,满足:![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为2的等比数列.
是公比为2的等比数列.
(1)若![]() ,求数列
,求数列![]() 的所有项的和
的所有项的和![]() ;
;
(2)若![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在正整数![]() ,满足
,满足![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)84;(2)1033;(3)存在,![]()
【解析】
(1)由题意可得:![]() ,
, ![]() 即为:2,4,6,8,10,12,14,16,8,4; 可得
即为:2,4,6,8,10,12,14,16,8,4; 可得![]() 的值;
的值;
(2)由题意可得![]() ,故有
,故有![]() ;即
;即![]() ,即
,即![]() 必是2的整数幂,要
必是2的整数幂,要![]() 最大,
最大,![]() 必需最大,
必需最大,![]() ,可得出
,可得出![]() 的最大值;
的最大值;
(3)由![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为2的等比数列,可得
是公比为2的等比数列,可得![]() 与
与![]() ,可得k与m的方程,一一验算k的值可得答案.
,可得k与m的方程,一一验算k的值可得答案.
解:(1)由已知![]() ,
,
故![]() 为:2,4,6,8,10,12,14,16;
为:2,4,6,8,10,12,14,16;![]() 公比为2,则对应的数为2,4,8,16,
公比为2,则对应的数为2,4,8,16,
从而![]() 即为:2,4,6,8,10,12,14,16,8,4;
即为:2,4,6,8,10,12,14,16,8,4;
此时![]()
(2)![]() 是首项为2,公差为2 的等差数列,
是首项为2,公差为2 的等差数列,
故![]() ,从而
,从而![]() ,
,
而![]() 首项为2,公比为2的等比数列且
首项为2,公比为2的等比数列且![]() ,
,
故有![]() ;即
;即![]() ,即
,即![]() 必是2的整数幂
必是2的整数幂
又![]() ,要
,要![]() 最大,
最大,![]() 必需最大,
必需最大,![]() ,故
,故![]() 的最大值为
的最大值为![]() ,
,
所以![]() ,即
,即![]() 的最大值为1033
的最大值为1033
(3)由数列![]() 是公差为
是公差为![]() 的等差数列知,
的等差数列知,![]() ,而
,而
![]() 是公比为2的等比数列,则
是公比为2的等比数列,则![]() ,故
,故![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,则
,则
![]() ,即
,即![]() ,则
,则![]() ,即
,即![]()
显然![]() ,则
,则![]() ,所以
,所以![]() ,将
,将![]() ,代入验证知,
,代入验证知,
当![]() 时,上式右端为8,等式成立,此时
时,上式右端为8,等式成立,此时![]() ,
,
综上可得:当且仅当![]() 时,存在
时,存在![]() 满足等式
满足等式


科目:高中数学 来源: 题型:
【题目】已知以点P为圆心的圆经过点A(-1,0)和B(3,4),线段AB的垂直平分线交圆P于点C和D,且|CD|=![]() .
.
(1)求直线CD的方程;
(2)求圆P的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取![]() 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于![]() 公里和
公里和![]() 公里之间,将统计结果分成
公里之间,将统计结果分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
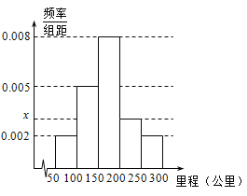
(1)求直方图中![]() 的值;
的值;
(2)求![]() 辆纯电动汽车续驶里程的中位数;
辆纯电动汽车续驶里程的中位数;
(3)若从续驶里程在![]() 的车辆中随机抽取
的车辆中随机抽取![]() 辆车,求其中恰有一辆车的续驶里程为
辆车,求其中恰有一辆车的续驶里程为![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
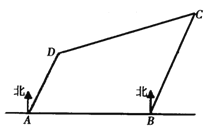
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
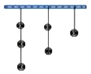
A.78B.60C.48D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x=1与x=2是函数f(x)=aln x+bx2+x的两个极值点.
(1)试确定常数a和b的值;
(2)判断x=1,x=2是函数f(x)的极大值点还是极小值点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com