
����Ŀ����ȥ������˲��ô���ķ�ʽ��Ǯ�����������Ա�֤�Լ�������ȶ������ǵ�ͨ�����͵�ѹ����������ǰ����е�Ǯ����������Ⲣ����һ�ֺܺõķ�ʽ�����Ž���ҵ�ķ�չ����ͨ���ܹ�ʹ�õ�Ͷ�����ƹ���Ҳ����������Ϊ���о�ij�����ƹ��ߵ�ʹ��������ֶ�![]() ����ε���Ա�����˵����о�����������������ֳ�5�飺
����ε���Ա�����˵����о�����������������ֳ�5�飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���������õ�Ƶ�ʷֲ�ֱ��ͼ��
���������õ�Ƶ�ʷֲ�ֱ��ͼ��
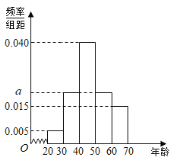
��1����ͼ�е�aֵ��
��2�����÷ֲ�����ķ������ӵڶ��顢�����顢�������й���ȡ8�ˣ����������У�����ȡ�����ˣ�
��3����Ƶ�ʷֲ�ֱ��ͼ�������б�������Ա��ƽ�����䣮
���𰸡���1��![]() ��2�����������γ�ȡ������Ϊ2��4��2��3����������Ա��ƽ������Ϊ47��
��2�����������γ�ȡ������Ϊ2��4��2��3����������Ա��ƽ������Ϊ47��
��������
��1������Ƶ��֮��Ϊ![]() ����ÿ���Ӧ����������Ӻ��ٳ���������
����ÿ���Ӧ����������Ӻ��ٳ���������![]() ���õ�
���õ�![]() ��ֵ����2�����ݵڶ������������Ƶ��֮�ȵõ��ֲ�����ı������ٵõ�ÿ������ȡ���������õ��𰸣���3������ÿ���м�ֵ��ÿ���Ƶ�ʵõ����б�������Ա��ƽ������.
��ֵ����2�����ݵڶ������������Ƶ��֮�ȵõ��ֲ�����ı������ٵõ�ÿ������ȡ���������õ��𰸣���3������ÿ���м�ֵ��ÿ���Ƶ�ʵõ����б�������Ա��ƽ������.
�⣺��1����Ƶ�ʷֲ�ֱ��ͼ�����ʿɵ�
![]() ��
��
���![]() ��
��
��2���ڶ��顢�����顢�������Ƶ�ʱ�Ϊ![]() ��
��
��Ϊ����ȡ![]() �ˣ�
�ˣ�
�������������γ�ȡ������Ϊ![]() ��
��![]() ��
��![]() ��
��
��3������Ƶ�ʷֲ�ֱ��ͼ�����ʣ�
ÿ����м�ֵ���Զ�Ӧ��Ƶ������ӣ��õ������ƽ��ֵ
![]()
�౻������Ա��ƽ������Ϊ![]() �꣮
�꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����g��x��=ax2��2ax+1+b��a��0��������[0��3]�������ֵ4����Сֵ1����f��x��=![]() ��
��
��1����a��b��ֵ��
��2��������ʽf��2x����k2x��0��x��[��1��1]���н⣬��ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪y��f(x)�ĵ�����f��(x)��ͼ����ͼ��ʾ�������н�����ȷ����(����)
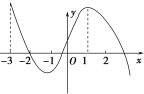
A.f(x)��(��3����1)���������B.x����2��f(x)��Сֵ��
C.f(x)��(��1,1)����������D.x��1�Ǻ���f(x)�ļ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OΪ����ԭ�㣬���ں���![]() ��������
��������![]() ����
Ϊ����![]() �İ���������ͬʱ�ƺ���
�İ���������ͬʱ�ƺ���![]() Ϊ����
Ϊ����![]() �İ��溯��.
�İ��溯��.
��1���躯��![]() ������
������![]() ��������
��������![]() ��
��
��2��������![]() �İ��溯��Ϊ
�İ��溯��Ϊ![]() ����
����![]() ��
��![]() ʱ
ʱ![]() ��ֵ��
��ֵ��
��3���ɣ�1���к���![]() ��ͼ�������겻�䣩�������쳤Ϊԭ����2�����ٰ�����ͼ������ƽ��
��ͼ�������겻�䣩�������쳤Ϊԭ����2�����ٰ�����ͼ������ƽ��![]() ����λ���ȵõ�
����λ���ȵõ�![]() ��ͼ����֪
��ͼ����֪![]() ��
��![]() ������
������![]() ��ͼ�����Ƿ����һ��P��ʹ��
��ͼ�����Ƿ����һ��P��ʹ��![]() .�����ڣ����P�����ꣻ�������ڣ�˵������.
.�����ڣ����P�����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() Ϊ��Բ��һ���㣨�������Ҷ��㣩����
Ϊ��Բ��һ���㣨�������Ҷ��㣩����![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ������������ֵΪ
������������ֵΪ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����![]() ����Բ
����Բ![]() �������㣬�߶�
�������㣬�߶�![]() ���е�Ϊ
���е�Ϊ![]() ��
��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]()
![]() Ϊ����ԭ��
Ϊ����ԭ��![]() ����
����![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼΪij�й����7����ڵ�¥���Ϲ�����ɽ���������ͼ��С��ͬѧ��������ͼ����7����Ϲ�������λ���ף���ɽ�������λ���ף����������жϣ����ճɽ�������λ����26�����ճɽ���������ƽ���ɽ�������2�죻���Ϲ�������������أ���10��2�յ�10��6���Ϲ����ķ�ɢ�̶ȱȳɽ����ķ�ɢ�̶ȸ���.�������ж������ĸ���Ϊ�� ��
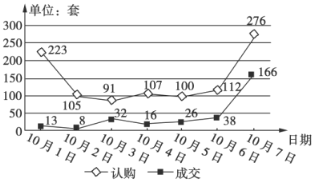
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������.ʤ��һ��1�֣�ƽһ�ֵ�0.5�֣���һ�ֵ�0�֡�����8��ѡ�ֽ��е�ѭ��������ÿ���˾���һ�֣���������ָ�ѡ�ֵĵ÷־�����ͬ�������÷��ɴ�С���к����κ�����ѡ�ֵ�4.5�֣��ڶ����ĵ÷ֵ����������ѡ�ֵ÷��ܺ�.��ǰ����ѡ�ָ��ö��ٷ֣�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2018����ԥ�Ͼ�У������ѧ�ڵ�һ���������躯��![]() ��
��
��I����![]() ʱ��
ʱ�� ![]() ���������
���������![]() �ķ�Χ��
�ķ�Χ��
��II����![]() ��
��![]() ��������Ϊ
��������Ϊ![]() ���ҷ���
���ҷ���![]() ǡ�����⣬��ʵ��
ǡ�����⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⣺
����������![]() ����
����![]() ���ķ�����Ϊ����
���ķ�����Ϊ����![]() ����
����![]() ����
����
����![]() ������
������![]() ���ı�Ҫ�����������
���ı�Ҫ�����������
��![]() ��������ʹ��
��������ʹ��![]() ���ķ��ǣ���
���ķ��ǣ���![]() ������
������![]() ����
����
����������![]() ����
����![]() �����������������
�����������������
����������ȷ����������________.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com