
| A. | $({1,\frac{5}{3}}]$ | B. | (1,2] | C. | $[{\frac{5}{3},+∞})$ | D. | [2,+∞) |
分析 由双曲线的定义可得|PF1|-|PF2|=3|PF2|=2a,再根据点P在双曲线的右支上,可得|PF2|≥c-a,从而求得此双曲线的离心率e的取值范围.
解答 解:∵|PF1|=4|PF2|,
∴由双曲线的定义可得|PF1|-|PF2|=3|PF2|=2a,
∴|PF2|=$\frac{2}{3}$a,
∵点P在双曲线的右支上,
∴|PF2|≥c-a,
∴$\frac{2}{3}$a≥c-a,即$\frac{5}{3}$a≥c,
∴e=$\frac{c}{a}$≤$\frac{5}{3}$,
∵e>1,
∴1<e≤$\frac{5}{3}$,
∴双曲线的离心率e的取值范围为(1,$\frac{5}{3}$].
故选:A.
点评 本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,考查学生的计算能力,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
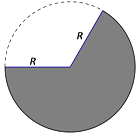 某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.
某工厂要生产体积为定值V的漏斗,现选择半径为R的圆形马口铁皮,截取如图所示的扇形,焊制成漏斗.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,0) | C. | (-2,-1] | D. | [-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,H为BC上异于B,C的任一点,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ=$\frac{1}{2}$.
如图,在△ABC中,H为BC上异于B,C的任一点,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-7)∪(1,+∞) | B. | (-∞,-7]∪[1,+∞) | C. | (-7,1) | D. | [-7,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com