
分析 依题意,通过分类讨论,得到$\left\{\begin{array}{l}{ax+2=0}\\{ln(x+a)=0}\end{array}\right.$时,(ax+2)•ln(x+a)≤0对x∈(-a,+∞)恒成立,解方程$\left\{\begin{array}{l}{ax+2=0}\\{ln(x+a)=0}\end{array}\right.$即可得到答案.
解答 解:∵x∈(-a,+∞),
∴当-a<x<1-a时,y=ln(x+a)<0,
当x>1-a时,y=ln(x+a)>0,
又(ax+2)•ln(x+a)≤0对x∈(-a,+∞)恒成立,
①若a>0,y=ax+2与y=ln(x+a)均为定义域上的增函数,
在x∈(-a,+∞)上,可均大于0,不满足题意;
②若a=0,则2lnx)≤0对x∈(0,+∞)不恒成立,不满足题意;
∴a<0.
作图如下:
由图可知,当且仅当方程为y=ln(x+a)的曲线与方程为y=ax+2的直线相交于点A,
即满足$\left\{\begin{array}{l}{ax+2=0}\\{ln(x+a)=0}\end{array}\right.$时,(ax+2)•ln(x+a)≤0对x∈(-a,+∞)恒成立,
解方程$\left\{\begin{array}{l}{ax+2=0}\\{ln(x+a)=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=-\frac{2}{a}}\\{x=1-a}\end{array}\right.$,解得a=-1.
故答案为:-1.
点评 本题考查函数恒成立问题,分析得到当$\left\{\begin{array}{l}{ax+2=0}\\{ln(x+a)=0}\end{array}\right.$时,(ax+2)•ln(x+a)≤0对x∈(-a,+∞)恒成立是关键,考查分类讨论思想与数形结合思想、等价转化思想的综合运用,考查逻辑思维与运算能力,属于难题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案科目:高中数学 来源: 题型:选择题
 如图,为测量塔高AB,选取与塔底B在同一水平面内的两点C、D,在C、D两点处测得塔顶A的仰角分别为45°,30°,又测得∠CBD=30°,CD=50米,则塔高AB=( )
如图,为测量塔高AB,选取与塔底B在同一水平面内的两点C、D,在C、D两点处测得塔顶A的仰角分别为45°,30°,又测得∠CBD=30°,CD=50米,则塔高AB=( )| A. | 50米 | B. | 25$\sqrt{3}$米 | C. | 25米 | D. | 50$\sqrt{3}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥β,则a∥b | B. | 若a?α,b?β,a∥b,则α∥β | ||
| C. | 若a∥b,b∥α,α∥β,则a∥β | D. | 若a⊥α,a⊥β,b⊥β,则b⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
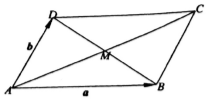
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | e1=e2<e3 | B. | e1<e2=e3 | C. | e1=e2>e3 | D. | e2=e3<e1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com