练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

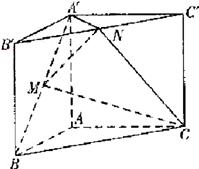
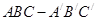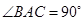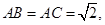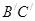    如图，直三棱柱，，AA′=1，点M，N分别为和的中点。

       (Ⅰ)证明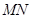：∥平面；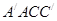

       (Ⅱ)求三棱锥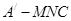的体积。（锥体体积公式V=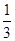Sh,其中S为底面面积，h为高）

     

    【答案】

    见解析

    【解析】（1）证法一：连结.由已知，

    AB=AC，三棱柱为直三棱柱，所以M为中点，

    又因为N为的中点，所以∥.

    又,,因此∥

    证法二：取中点P，连结MP,NP，而M，N分别为的中点，所以MP∥，PN∥，所以MP∥，PN∥，又,

    因此∥.而，因此MN∥

    （2）解法一：连结BN，由题意，，所以.

    又，故.

    解法二：.

    考点定位：本大题主要以三棱柱为几何背景考查线面平行的判定和椎体体积的求法，突出考查空间想象能力和计算能力

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其左视图的面积为（　　）
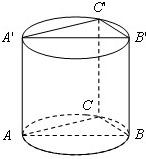    精英家教网
    A、4
    B、
    		3
    C、2
    		3
    D、2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，直三棱柱ABC-A′B′C′内接于高为
    		2
    的圆柱中，已知∠ACB=90°，AA′=
    		2
    ，BC=AC=1，O为AB的中点．
    求（1）圆柱的全面积；
    （2）异面直线AB′与CO所成的角的大小；
    （3）求二面角A′-BC-A的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，直三棱柱ABB1-DCC1中，∠ABB1=90°，AB=4，BC=2，CC1=1，DC上有一动点P，则△APC1周长的最小值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

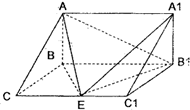    精英家教网如图，直三棱柱ABC-A1B1C1中，AB⊥BC，E为棱CC1的中点，已知AB=
    		2
    ，BB1=2，BC=1．
    （1）证明：BE是异面直线AB与EB1的公垂线；
    （2）求二面角A-EB1-A1的大小；
    （3）求点A1到面AEB1的距离．

    查看答案和解析>>

    科目：高中数学 来源：2013届新课标高三配套第四次月考文科数学试卷（解析版） 题型：解答题

    如图，直三棱柱ABC－A′B′C′，∠BAC＝90°，AB＝AC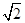＝，AA′＝1，点M，N分别为A′B和B′C′的中点.

    （1）证明：MN∥平面A′ACC′；

    （2）求三棱锥A′－MNC的体积.

    （锥体体积公式V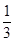＝Sh，其中S为底面面积，h为高）

     

    查看答案和解析>>

    同步练习册答案