Question

已知二面角α-l-β的大小为45°，m，n为异面直线，且m⊥α，n⊥β，则m，n所成角的大小为

1. A.
   135°
2. B.
   90°
3. C.
   60°
4. D.
   45°

Answer 1

D
分析：在直线m上取点P，过P作PA⊥β于A，结合n⊥β可得PA∥n，直线PA与m所成的锐角或直角就是m，n所成角．设m⊥α于B，经过点P、A、B的平面交二面角α-l-β的棱l于C，连接AC、BC．利用直线与平面垂直的判定与性质，可得∠ACB即为二面角α-l-β的平面角，即∠ACB=45°，最后用四边形内角和定理，得到∠APB=180°-∠ACB=135°，PA与m所成的锐角是45°，因此m，n所成角的大小为45°．
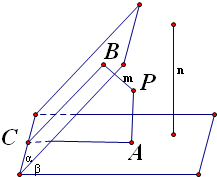
解答：在直线m上取点P，过P作PA⊥β于A，设m⊥α于B
作出经过点P、A、B的平面，该平面交二面角α-l-β的棱l于C
连接AC、BC
∵PA⊥β，n⊥β
∴PA∥n，直线PA与m所成的锐角或直角就是m，n所成角
∵PA⊥β，l⊆β
∴l⊥PA
同理l⊥PB
∵PA∩PB=P
∴l⊥平面PAB
∵AC、BC?平面PAB
∴l⊥AC，l⊥BC
∠ACB即为二面角α-l-β的平面角，∠ACB=45°
∵四边形PACB中，∠PAC=∠PBC=90°
∴∠APB=180°-∠ACB=135°
∴PA与m所成的锐角为180°-135°=45°
所以异面直线m，n所成角等于45°
故选D
点评：本题着重考查了异面直线所成角、二面角的平面角的作法和直线与平面垂直的判定与性质等知识点，属于中档题．运用垂面法作二面角的平面角，是解决本题的关键．