
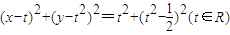 ,圆C过y轴上的定点A,线段MN是圆C在x轴上截得的弦,设|AM|=m,|AN|=n.对于下列命题:
,圆C过y轴上的定点A,线段MN是圆C在x轴上截得的弦,设|AM|=m,|AN|=n.对于下列命题: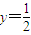 相切;
相切;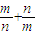 的取值范围是
的取值范围是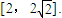
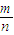 +
+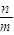 ≥2,由余弦定理求出 cosA,由三角形的面积可求 sinA,再运sinA+cosA≤
≥2,由余弦定理求出 cosA,由三角形的面积可求 sinA,再运sinA+cosA≤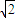 ,可得
,可得 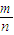 +
+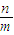 ≤2
≤2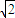 .
.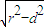 =2
=2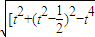 =2
=2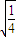 =1,故②正确.
=1,故②正确.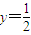 的距离等于|t2-
的距离等于|t2- |,而半径为
|,而半径为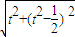 ,二者不一定相等,故③不正确.
,二者不一定相等,故③不正确. =0,∴x=t2+
=0,∴x=t2+ 或 x=t2-
或 x=t2- ,
, ,0),N(t2-
,0),N(t2- ,0),由圆C方程知A(0,
,0),由圆C方程知A(0, ),
),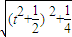 ,|AN|=n=
,|AN|=n=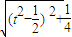 ,
, +
+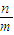 ≥2(当且仅当m=n时等号成立),
≥2(当且仅当m=n时等号成立),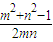 ,
, •m•n•sinA=
•m•n•sinA= ×1×
×1× ,∴sinA=
,∴sinA=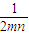 ,
,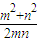 ≤
≤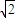 ,∴
,∴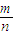 +
+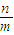 =
=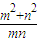 ≤2
≤2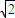 ,
,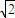 ≥
≥ +
+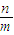 ≥2,故④正确.
≥2,故④正确. 这个结论.
这个结论. 

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| n |
| n |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源:陕西部分学校2008年5月高三联合测试、理科数学测题 题型:013
已知向量![]() 若向量
若向量![]() 与
与![]() 的夹角为60°,则直线
的夹角为60°,则直线![]() 与圆
与圆![]() 的位置关系系是
的位置关系系是
A.相交
B.相切
C.相离
D.相交且过圆心
查看答案和解析>>
科目:高中数学 来源:2013届四川省巴中市四县中高二上学期期末考试理科数学 题型:填空题
已知圆系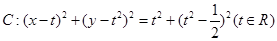 。圆C过
。圆C过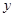 轴上的点A,线段MN是圆C在
轴上的点A,线段MN是圆C在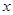 轴上截得的弦。设
轴上截得的弦。设 ,对于下列命题:
,对于下列命题:
①不论t取何实数,圆心C始终在曲线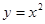 上;
上;
②不论t取何实数,弦MN的长为定值1;
③不论t取何实数,圆系C的所有圆都与直线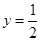 相切;
相切;
④式子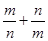 的取值范围是
的取值范围是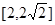 。
。
其中所有正确命题的序号是________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com