
分析 利用正弦定理求出C,法一:求出三角形的外接圆的半径,然后利用两角和以及正弦定理求出a+b+c的取值范围.
法二:利用余弦定理化简求解即可.
解答 解:由$acosB+bcosA=\frac{{\sqrt{3}c}}{2sinC}$,得$sinAcosB+sinBcosA=\frac{{\sqrt{3}sinC}}{2sinC}$,
即$sin(A+B)=sinC=\frac{{\sqrt{3}}}{2}$,因为角C是锐角,所以$C=\frac{π}{3}$.
(接上)法一:所以$A+B=\frac{2π}{3}$,$2R=\frac{c}{sinC}=\frac{2}{{sin\frac{π}{3}}}=\frac{{4\sqrt{3}}}{3}$
所以$a+b+c=2R(sinA+sinB+sinC)=\frac{{4\sqrt{3}}}{3}(sinA+sin(\frac{2π}{3}-A)+sin\frac{π}{3})=4cos(A-\frac{π}{3})+2$
又因为 $0<A<\frac{2π}{3}$,所以 $-\frac{π}{3}<A-\frac{π}{3}<\frac{π}{3}$,所以 $\frac{1}{2}<cos(A-\frac{π}{3})≤1$
所以 $4<4cos(A-\frac{π}{3})+2≤6$,所以 4<a+b+c≤6.
法二:由余弦定理得${c^2}={a^2}+{b^2}-2abcos\frac{π}{3}={(a+b)^2}-3ab≥{(a+b)^2}-\frac{{3{{(a+b)}^2}}}{4}=\frac{{{{(a+b)}^2}}}{4}$
当且仅当a=b时等号成立.由(a+b)2≤16,得a+b≤4,
又 a+b>c,且c=2,所以4<a+b+c≤6.
故答案为:(4,6].
点评 本题考查正弦定理以及余弦定理的应用,考查三角形的解法.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3} | B. | {4} | C. | {3,4} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
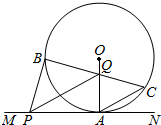 如图,⊙O的半径为r,MN切⊙O于点A,弦BC交OA于点Q,BP⊥BC,交MN于点P
如图,⊙O的半径为r,MN切⊙O于点A,弦BC交OA于点Q,BP⊥BC,交MN于点P查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com