练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在以下关于向量的命题中，不正确的是（　　）
    A、若向量
    a
    =（x，y），向量
    b
    =（-y，x）（x，y≠0），则
    a
    ⊥
    b
    B、在△ABC中，
    AB
    和
    CA
    的夹角等于角A
    C、四边形ABCD是菱形的充要条件是
    AB
    =
    DC
    ，且|
    AB
    |=|
    AD
    |
    D、点G是△ABC的重心，则
    GA
    +
    GB
    +
    GC
    =
    0
    分析：根据向量数量积判断两个向量的垂直关系的方法，我们可以判断A的真假；根据向量夹角的定义，我们可以判断B的真假；根据菱形的定义及相等向量及向量的模的概念，我们可以判断C的真假；根据三角形重心的性质，可判断D的真假，进而得到答案．
    解答：解：若向量
    a
    =（x，y），向量
    b
    =（-y，x），则
    a
    •
    b
    =0，则
    a
    ⊥
    b
    ，故A正确；
    在△ABC中，
    AB
    和
    CA
    的夹角等于角A的补角，故B错误；
    由菱形是邻边相等的平行四边形，故四边形ABCD是菱形的充要条件是
    AB
    =
    DC
    ，且|
    AB
    |=|
    AD
    |，故C正确；
    由重心的性质，易得
    GA
    +
    GB
    +
    GC
    =
    0
    ?G是△ABC的重心，故D正确；
    故选B
    点评：本题考查的知识点是向量的夹角，数量积判断两个向量的垂直关系，相等向量与向量的模，是对向量基本概念和基本方法的直接考查，属于基础题型，难度不大，熟练掌握相关概念和方法即可解答．D中应该G是△ABC的重心，则
    GA
    +
    GB
    +
    GC
    =
    0
    ！！
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在以下关于向量的命题中，不正确的是（　　）
    A、若向量a=（x，y），向量b=（-y，x），（xy≠0），则a⊥b
    B、平行四边形ABCD是菱形的充要条件是（
    AB
     +
    AD
    ）（
    AB
    -
    AD
    ）=0
    C、点G是△ABC的重心，则
    GA
    +
    GB
    +
    CG
    =
    0
    D、△ABC中，
    AB
    和
    CA
    的夹角等于180°-A

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在以下关于向量的命题中，不正确的是（　　）
    A、若向量
    a
    =(1，2)，向量
    b
    =(-2，1)，则
    a
    ⊥
    b
    B、△ABC中，有
    AB
    +
    BC
    =
    AC
    C、△ABC中
    AB
    和
    CA
    的夹角为角A
    D、已知四边形ABCD，则四边形ABCD是菱形的充要条件是
    AB
    =
    DC
    ，且    |
    AB
    |=|
    AD
    |

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年湖北省高三2月调研考试数学理卷 题型：选择题

    在以下关于向量的命题中，不正确的是（    ）

    A．若向量a=(x，y)，向量b=(－y，x),  (x y≠ 0 )，则a⊥b

    B．平行四边形ABCD是菱形的充要条件是.

    C．点G是△ABC的重心，则++=

    D．△ABC中，和的夹角等于180°－A

     

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年深圳高级中学高二下学期期末测试数学（理） 题型：选择题

    在以下关于向量的命题中，不正确的是                       

    A．若向量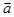=（x, y），向量=(－y,x) (xy≠0)，则⊥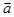

    B．已知四边形ABCD，则四边形ABCD是菱形的充要条件是

    C．点G是△ABC的重心，则   

    D．△ABC中，的夹角为角A

     

    查看答案和解析>>

    同步练习册答案